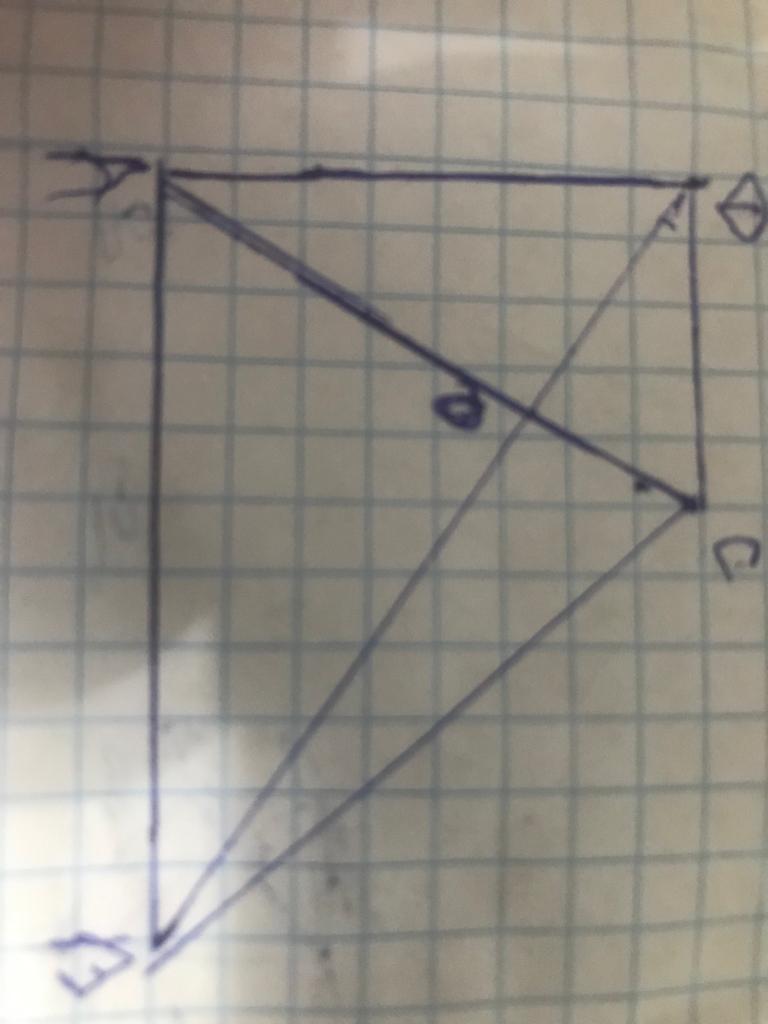
Геометрия, вопрос задал qabilcavadov25 , 1 год назад

65. Диагонали прямоугольной трапеции ABCD (<А=90градусов) взаимно перпендикулярны.
Найдите длину отрезка DC,если AB=28,AD=14

Ответы на вопрос

Ответил zanbolkobeev999

1

Ответ: DC=7

Объяснение:

Пусть АС∩BD=O. тогда АО-высота. Из треугольника АВС=> $AD^2=DB*DO\\AB^2=DB*OB\\\frac{AD^2}{AB^2}=\frac{DO}{OB} =(\frac{1}{2})^2 =\frac{1}{4} \\$

треугольник AOB подобен треугольнику COD , так как ∠АОВ=∠СОD - как вертикальные и ∠ОАВ=∠OCD как накрест лежащие=> $\frac{DC}{AB}=\frac{DO}{OB}= > DC=AB*\frac{DO}{OB}=28*\frac{1}{4}=7$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 11 месяцев назад

Коля пишет на доске последовательность натуральных чисел. Первое число N > 1 написано заранее. Новые натуральные числа он получает так: вычитает из последнего записанного числа или прибавляет к...

Математика, 11 месяцев назад

Тимофій має сад у формі квадрата зі стороною 9 м . яка довжина паркану, що огороджують цей сад...

Русский язык, 1 год назад

Замени словосочетание «собачьи уши», построенное на основе согласования, синонимичным словосочетанием со связью управление. Напиши получившееся словосочетание.

Математика, 1 год назад

В файле два задания, помогите решить...

Геометрия, 6 лет назад

ДАЮ 10 БАЛЛОВ, ЕЩЁ ОДНА ЗАДАЧА В ПРОФИЛЕ...

География, 6 лет назад

сарезьке озеро за походженням улоговин? ТОЧНЫЙ ОТВЕТ...