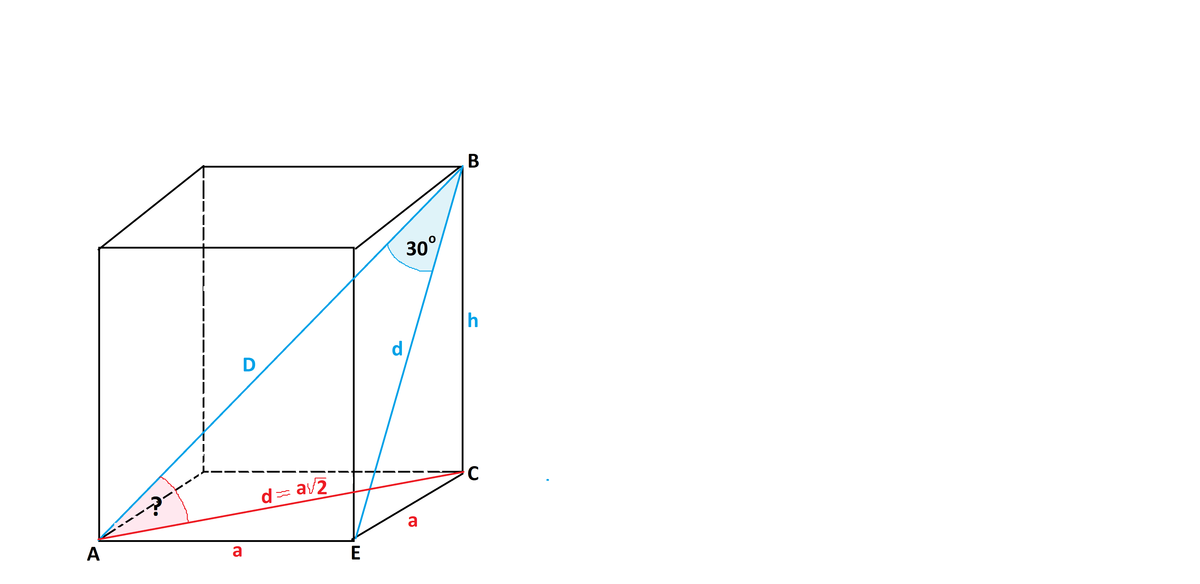
2. Сторона основания правильной четырехугольной призмы равна а . Диагональ призмы наклонена к плоскости боковой грани под углом 300. Найти высоту призмы и угол наклона диагонали призмы к плоскости основания.
Ответы на вопрос
Сторона основания правильной четырехугольной призмы равна а .
Диагональ призмы наклонена к плоскости боковой грани под углом 30°
Найти высоту призмы и угол наклона диагонали призмы к плоскости основания.
Ясно, что угол наклона диагонали к плоскости боковой грани равен 30°.
Сделаем и смотрим рисунок.
ВС- высота призмы.
АВ- ее диагональ.
ВЕ- диагональ боковой грани.
АЕ=ЕС= а - стороны основания.
Призма правильная. Значит, в основании - квадрат.
Угол АВЕ=30°
Диагональ основания АС= а√2 по формуле диагонали квадрата.
Диагональ АВ призмы = АЕ:sin (30°)=2a
Диагональ ВЕ боковой грани=АЕ:tg(30°)=а:(1/√3)=а√3
Высота ВС= h призмы по т.Пифагора
h²=(а√3)²-а²=2а²
h=а√2
Треугольник АВС - прямоугольный, в котором катеты АС=ВС.
Отсюда угол угол наклона диагонали призмы к плоскости основания
∠ ВАС=45°