11 класс Тіла обертання. Площі бічної та поєної поверхонь тіл обертання.

Відповідь:

1)10 2)200п см² 3)1924п см² 4)Радіус основи - 14√3 см; Твірна конуса - 28 см; Діаметр конуса - 28√3 см. 5)10 см.

Пояснення:

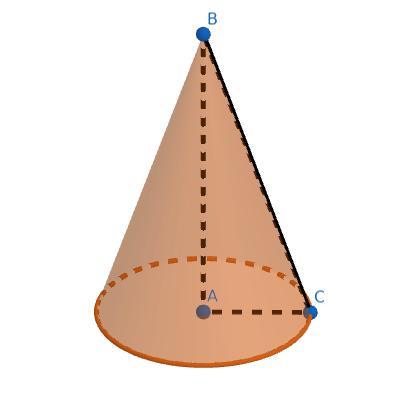
1)(Дивимось на 1 зображення) Нехай радіус конуса - сторона AC, AC=5см. BA - висота конуса, BC - твірна. Тоді кут ABC = 30ᵒ (Томущо це кут між висотою BA та твірною BC). У нас утворився прямокутний трикутник ABC, нам потрібно знайти BC, яка є гіпотенузою.В прямокутному трикутнику катет, що лежить проти кута трицять градусів у двічі менший за гіпотенузу, в нас є такий катет - AC, який за сумісництвом - радіус, який дорівнює 5см.

BC=2AC=2*5=10.

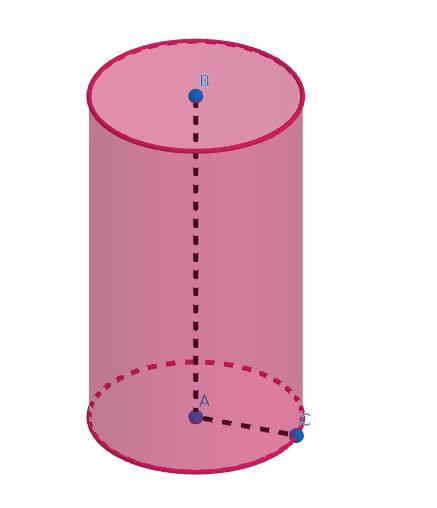
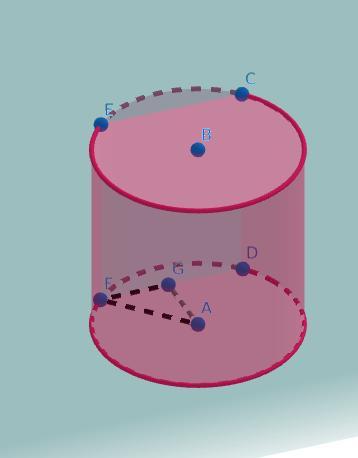
2)Дивимось на другий малюнок. Повна поверхня циліндра знаходиться за формулою: Sповна = Sбіч. + 2*Sосн. (Ми беремо бічну площу і додаємо 2 площі основи (їх 2 тому, що в циліндра зверху і знизу однакова основа))

Щоб знайти Sбіч. ми маємо взяти довжину кола основи(яка знаходиться за формулою 2пR) і помножити її на висоту (2п*R*h):

Радіус в нас AC, AC=5 см. Ну а висота - AB, AB=15 см:

2п*AC*AB=2п*5*15=2п*75=150п

Основа циліндра - коло, площа кола знаходиться: пR²,  Радіус ми маємо (5см), знаходимо: Sосн = п*5²=п25=25п

Sповн=150п + 2*25п=200п (см²)

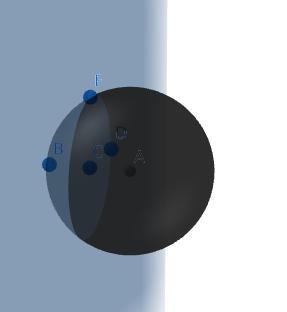
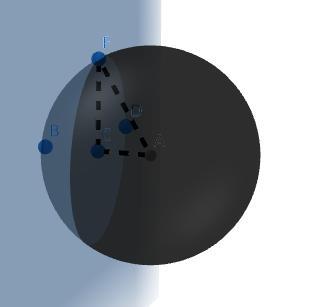
3)Переріз кулі площиною виглядає як на 3 зображенні. Щоб знайти його площу - потрібно знайти площу кола, яке утворилось. (Ось цього із центром у точці C, і з діаметром CF) Для цього нам потрібно знайти його діаметр, CF. На малюнку ясно видно, що AF - діаметр кулі, тобто AF=50см. Також ми бачимо, що CA - є відстанню площини до центра кулі, тобто CA=24 см. Дивимось на 4 зображення у нас утворився прямокутний трикутник ACF (∠С=90ᵒ), У нас є гіпотенуза AF та катет AC, використовуємо теорему піфагора:

AF²=CA²+CF²

50²=24²+CF²

50²-24²=CF²

1924=CF²

Тепер, коли ми отримали діаметр перерізу (який є колом) шукаємо його площу за формою площі кола: S=п*R²=п*CF²=п*1924=1924п (см²)

4)Вершина конуса - SO, SO=12см. Кут при вершині осьового перерізу - це ASB, (доречі кути SAB та SBA - це кути при основі осьового перерізу) ∠ASB = 120ᵒ. Спочатку ми знайдемо твірну (сторону SA): Трикутник ASO - прямокутний (∠O=90ᵒ). Ми розуміємо, що кут ASO дорівнює половині ASB, тобто половині 120ᵒ, тобто 60ᵒ. Ми маємо 2 кути (SOA та ASO), можемо знайти третій. Сума кутів в трикутнику має дорівнювати 180ᵒ:

∠SOA+∠ASO+∠SAO=180ᵒ

90ᵒ+60ᵒ+∠SAO=180ᵒ

∠SAO=180ᵒ-90ᵒ-60ᵒ=30ᵒ

Одже кут SAO дорівнює 30ᵒ. Тепер увага: в прямокутному трикутнику катет, що лежить проти кута 30ᵒ в два рази менший за гіпотенузу.

Кут 30ᵒ - це SAO, катет, що лежить проти нього - це SO. SO=14, він в два рази менший за гіпотенузу (AS), тобто гіпотенуза в два рази більша за нього: SA=2*SO=2*14=28.

Ось і твірна. Тепер знайдемо радіус основи (AO). За теоремою піфагора:

SA²=SO²+AO²

28²=14²+AO²

28²-14²=AO²

588=AO²

AO =

Ну а діаметр - це AB, діаметр дорівнює двом радіусам: AB=AO*2=

5)Дивимось на 5 зображення: Із малюнка видно, що переріз циліндра - це квадрат DCEF, одна із сторін якого (CD або EF) є висотою, її нам потрібно знайти. Маючи площу квадрата перерізу ми можемо поділити її на іншу сторону (FD) і отримати шукану CD (висоту). Шукаємо FD.

AG - відстань від перерізу до осі, яка дорівнює 8см. AF - радіус, який дорівнює 10 см. У нас утворився прямокутний трикутник AGF (∠G=90ᵒ), За теоремою піфагора знаходимо FG:

AF²=AG²+FG²

10²=8²+FG²

10²-8²=FG²

100-64=FG²

36=FG²

6=FG

На малюнку ми бачимо, що FG - половина FD, тому: FD=2*FG=2*6=12.

Повертаємось до нашого перерізу, який є прямокутником: Площа прямокутника дорівнює добутку двох сусідніх сторін (Наприклад EF і FD):

EF*FD=120см²

EF*12=120см²

EF=120/12

EF=10см.

EF і є висота, і вона дорівнює 10см.

Нажаль в одну відповідь я можу прикріпити тільки 5 малюнків, а далі без малюнків буде незрозуміло. Тому на цьому моя відповідь закінчена, будь ласка не видаляйте відповідь, можливо вона буде комусь корисна. Можете зробити нове питання (із 6, 7 завданнями).