Алгебра, вопрос задал villiwonkka1 , 6 лет назад

1.
Найдите промежутки возрастания и убывания:
$f (x) = x ^{3} - 12 {x}^{2} - 17x - 23$
2.
Найдите стационарные точки:
$f(x) = 3 {x}^{2} - 7x + 9$
3. Найдите локальные максимумы и минимумы функции:
$f(x) = x^{4} - 3 {x}^{3} + {x}^{2} + 9$
P.s Подробное решение.

Ответы на вопрос

Ответил natalyabryukhova

Ответ:

Объяснение:

1. Найдите промежутки возрастания и убывания:

Найдем производную, приравняем к нулю, найдем корни.

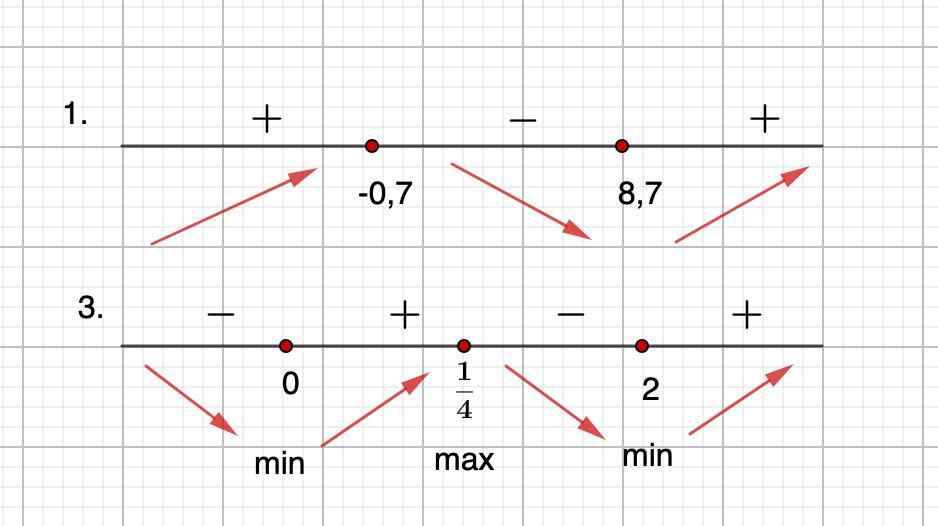
Определим знаки производной на промежутках. Если "+", функция возрастает, "-" - убывает.

$f(x)=x^3-12x^2-17x-23\\\\f'(x)=3x^2-12*2x-17=3x^2-24x-17\\\\f'(x)=0;\;\;\;3x^2-24x-17=0\\\\x_{1,2}=\frac{24^+_-\sqrt{576+204} }{6}=\frac{24^+_-2\sqrt{195} }{6}=\frac{12^+_-\sqrt{195} }{3} \\\\x_1=\frac{12+\sqrt{195} }{3}\approx 8,7;\;\;\;x_2=\frac{12-\sqrt{195} }{3}\approx -0,7$

См. рис.

Функция возрастает при х ∈ [-∞; -0,7]∪[8,7; +∞]

или

$\displaystyle x\in [- \infty ;\;\frac{12-\sqrt{195} }{3} ]\cup [\frac{12+\sqrt{195} }{3};\;+ \infty ]$

Функция убывает при х ∈ [-0,7; 8,7]

или

$\displaystyle x\in[\frac{12-\sqrt{195} }{3};\;\frac{12+\sqrt{195} }{3} ]$

2. Найдите стационарные точки:

Точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.

$\displaystyle f(x)=3x^2-7x+9\\\\f'(x)=6x-7\\\\f'(x)=0;\;6x-7=0\\\\x=\frac{7}{6}\\\\x= 1\frac{1}{6}$

3. Найдите локальные максимумы и минимумы функции.

Найдем производную, приравняем к нулю, найдем корни.

Определим знаки производной на промежутках. Если производная меняет знак с "+" на "-", то будет точка максимума. Если производная меняет знак с "-" на "+" - точка минимума.

$\displaystyle f(x)=x^4-3x^3+x^2+9\\\\f'(x)=4x^3-9x^2+2x\\\\f'(x)=0;\;\;\;x(4x^2-9x+2)=0\\\\x_1 = 0\\\\x_{2,3}=\frac{9^+_-\sqrt{81-32} }{8}=\frac{9^+_-7}{8}\\\\x_2=\frac{9+7}{8}=2;\;\;\;x_3=\frac{9-7}{8}=\frac{1}{4}$