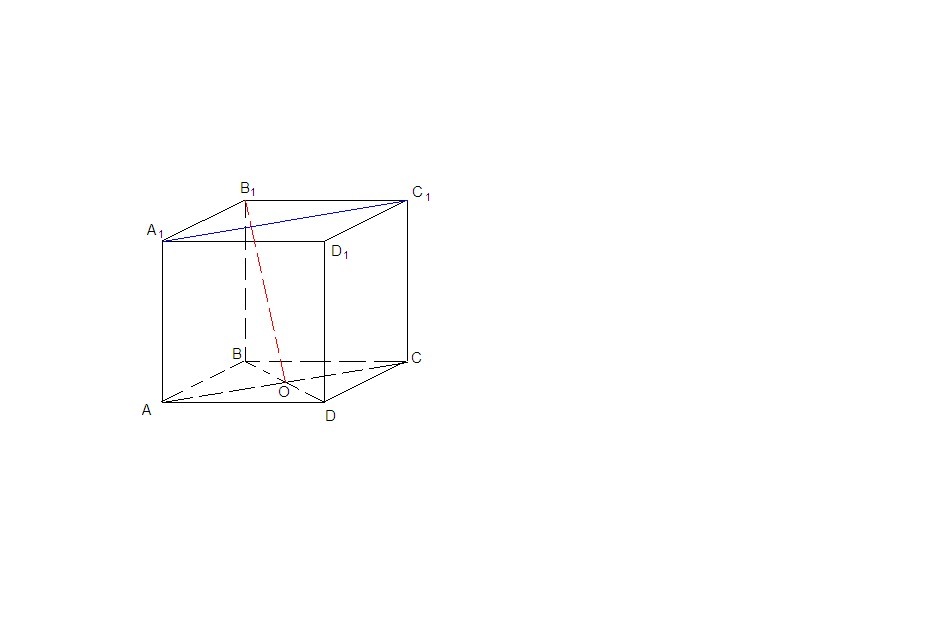
1)Дан куб ABCDA1B1C1D1 . О-точка пересечения диагоналей ABCD. Докажите , что прямые B1O и A1C1 перпендикулярны.

A₁C₁ лежит в плоскости А₁В₁С₁, прямая B₁O пересекает эту плоскость в точке В₁, не лежащей на прямой А₁С₁, значит эти прямые скрещивающиеся.

АА₁║СС₁ и АА₁ = СС₁, АА₁⊥А₁В₁С₁, а значит и А₁С₁, ⇒

АА₁С₁С - прямоугольник, ⇒ АС║А₁С₁.

Тогда угол между прямыми АС и В₁О равен искомому углу между прямыми А₁С₁ и В₁О.

BD⊥АС как диагонали квадрата, ⇒ и ВО⊥АС,

ВО - проекция В₁О на плоскость основания, значит и В₁О⊥АС по теореме о трех перпендикулярах.

Значит В₁О⊥А₁С₁.