Математика, вопрос задал Max8285 , 1 год назад

....................

Приложения:

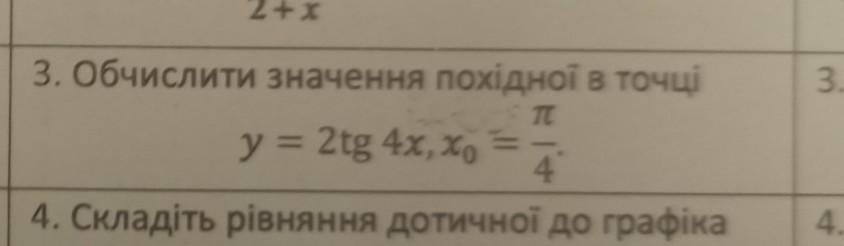
Ответы на вопрос

Ответил reygen

Ответ: 8

Пошаговое объяснение:

Вычислите значение производной в точке

$y = 2 \mathrm{tg }4x ~ ~ ; ~~ x_0 = \dfrac{\pi }{4}$

Производная сложной функции

( f(g(x)) )' = f'(g(x))·g'(x)

Тогда
$y' = (2\mathrm {tg }~4x)'= 2\cdot \dfrac{1}{\cos ^2 4x} \cdot (4x)' = \dfrac{8}{\cos ^24x }$

$y'(\frac{\pi }{4} ) = \dfrac{8}{\cos ^2 (4\cdot \frac{\pi }{4} ) } = \dfrac{8}{\cos^2 \pi } = \dfrac{8}{(-1)^2} = 8$

Ответил сок111213

$y=2\tan 4x\\y'=\frac{2\times4}{\cos^{2} 4x}=\frac{8}{\cos^{2} 4x}\\y'(\frac{\pi}{4})=\frac{8}{\cos^{2}( 4\times\frac{\pi}{4})}=\frac{8}{\cos^{2} \pi}=\frac{8}{(-1)^{2}}=8$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 11 месяцев назад

Контрольний письмовий твір опис місцевості на основі особистих вражень у художньому стилі...

Математика, 11 месяцев назад

знайдіть значення виразу: 0,4×(-5)⁴; 2) 25-4³+(-1)⁵...

Українська література, 1 год назад

Мотив братовбивства наявний у якому творі : А «Пам’яті тридцяти» Б «Одчиняйте двері...» Г «У теплі дні збирання винограду...» В «Ви знаєте, як липа шелестить...» Д «Ніч... а човен — як...

Геометрия, 1 год назад

6.(3 бала) Із даної точки А до площини проведено дві похилі АВ і AD та перпендикуляр АО. Проекції похилих на площину дорівнюють 7см і 18см. Знайдіть АО, якщо AB : AD = 5:6.

Математика, 6 лет назад

решите что отмечено галочкой...

Биология, 6 лет назад

Что способствует лучшему расщеплению крахмала клубней картофеля ферментами слюны? 1) кислая среда в полости рта I 2) употребление его горячем виде 3) тщательное его пережёвывание 4)...

....................​

Ответы на вопрос

( f(g(x)) )' = f'(g(x))·g'(x)

....................