.................................
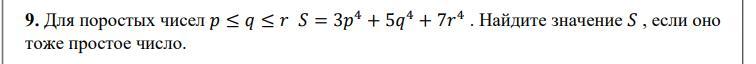
Ответы на вопрос
Ответ:
5023.
Пошаговое объяснение:
простые числа,
простое.
1) Сразу отбрасываем случай p=q=r, так как иначе S делилось бы на p и было бы составным.
2) Если p=2, q>p⇒ q и r нечетные, а тогда S - четное большее 2, то есть составное.
3) Если p=q=2, r=3 ⇒ делится на 5, то есть составное.
4) Если p=q=2, r>3 (то есть r=3k±1)⇒
делится на 3, то есть составное.
На этом закончен разбор случая p=2.
5) Если p=q=3, r=5⇒ S=5023. Поскольку достаточно проверить делимость этого числа на простые числа, меньшие 71, то есть на 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67. В принципе эти числа можно было найти с помощью решета Эратосфена (если необходимо, можете почитать о нем в интернете).
Непосредственная проверка показывает, что 5023 не делится ни на одно из этих чисел и поэтому является простым числом.
6) Если p=q=3, r>5 (то есть r=5k±1 или r=5k±2⇒ , то
делится на 5, то есть составное.
7) Если q>3 (а тогда и r>3)⇒
делится на 3, то есть составное.
На этом рассмотроение всех возможных случаев закончено.