Алгебра, вопрос задал FaerVator , 2 года назад

Помогите , пожалуйста , с подробно-пошаговым объяснением!

Приложения:

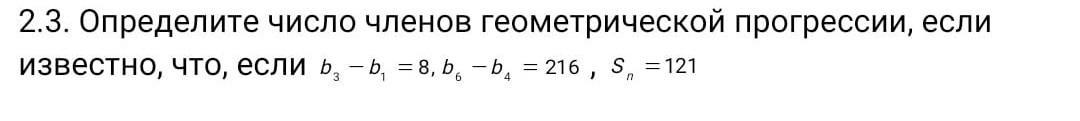
Ответы на вопрос

Ответил Jaguar444

1

ОтветОтвет:

n = 5

Объяснение:

Дано: b₃ – b₁ = 8, b₆ – b₄ = 216, Sₙ = 121

Найти: n - ?

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение

Составим систему.

$\displaystyle \left. \begin{cases} { b_3-b_1=8 } \\ { b_6-b_4=216 } \end{cases} \right.$

Воспользуемся формулой n-го члена геометрической прогрессии: $\displaystyle\boxed{\tt b_n=b_1\:*\:q^{n-1}}$

$\displaystyle b_3 = b_1\:*\: q^{2}$

$\displaystyle b_6=b_1\:*\:q^{5}$

$\displaystyle b_4 = b_1 \:*\: q^{3}$

Теперь переходим к системе.

$\left. \begin{cases} { b_1\:*\:q^{2}-b_1=8 } \\ {b_1\:*\:q^{5}-b_1\:*\:q^{3}=216 } \end{cases} \right.\\$

В первой уравнении вынесем за скобки b₁, во второй b₁ * q³.

$\left. \begin{cases} { b_1(q^{2}-1)=8 } \\ {b_1q^{3}(q^{2}-1)=216 } \end{cases} \right.\\$

Делим второе уравнение на первое и получим:

$\displaystyle q^{3}=27$

$\displaystyle q= \sqrt[3]{27}$

$\displaystyle q=3$

Чтобы найти первый член(b₁) подставим знаменатель в первое уравнение, либо во второе. Я предпочту первое.

$\displaystyle b_1 \:*\: 3^{2}-b_1=8$

$\displaystyle b_1 \:*\: 9-b_1=8$

$\displaystyle 9b_1 -b_1=8$

$\displaystyle 8b_1 =8 |:8$

$\displaystyle b_1 =1$

Теперь с помощью формулы суммы n первых членов геометрической прогрессии найдем число членов нашей прогрессии. $\displaystyle \boxed{\tt S_n = \frac{b_1(q^{n}-1)}{q - 1}}$

$\displaystyle 121 = \frac{1(3^{n}-1)}{3 - 1}$

$\displaystyle 121 = \frac{3^{n}-1}{2}$

$\displaystyle 121 \:*\:2= 3^{n}-1$

$\displaystyle 242= 3^{n}-1$

$\displaystyle 242+1= 3^{n}$

$\displaystyle 243= 3^{n}$

Теперь стоит задуматься, 3 в какой степени даст 243. Конечно же в 5 - ой степени.

$\displaystyle 3^{5}= 3^{n}$

$\displaystyle \bf n= 5$

FaerVator: спасибо!

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

сколько слогов в слове "радостного"...

Английский язык, 1 год назад

Нужно составить вопросы к диалогу ..... with your parents? Ответ: yes , and my sister. What about you? ..... any brothers and sisters? I have a brother. He's 19. ....... work? No,...

Английский язык, 2 года назад

2 ★★ Complete the sentences with the words in bold from the text. 1. Му раrents always _encourage_ me to try lots of different activities. 2. І must _____ you. I don't want to see you cheating. 3.

Русский язык, 2 года назад

Как сделать домашний задание...

Физика, 7 лет назад

Розвяжіть будь ласка задачу.тиск води на дно акваріума становить 6 кПа,площа дна 0,3 м2. Чому дорівнює сила тиску води на дно?

Физика, 7 лет назад

На проводник длиной 0,5 м, расположенный в магнитном поле ,действует сила 0,15 Ньютон. Найти силу тока в проводнике...