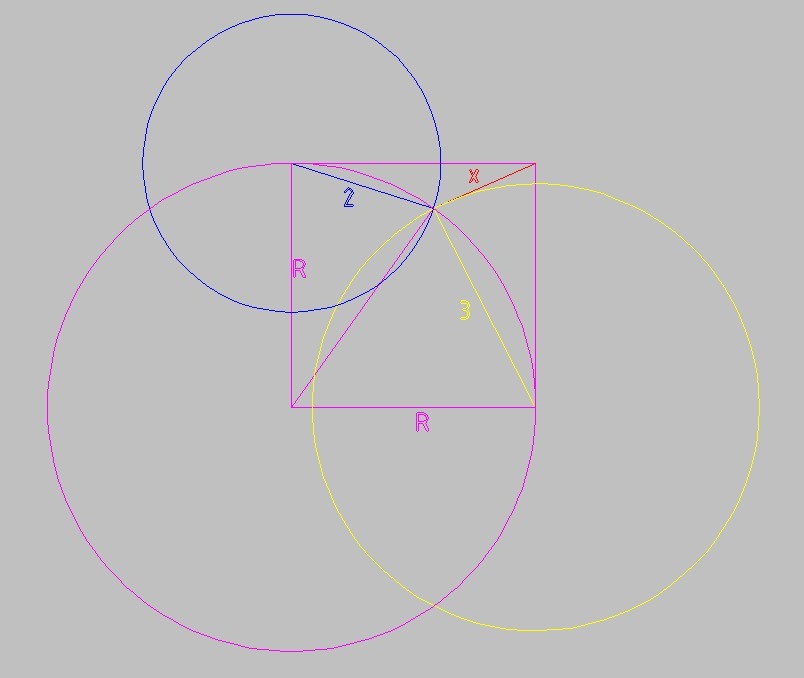...........................
Ответы на вопрос
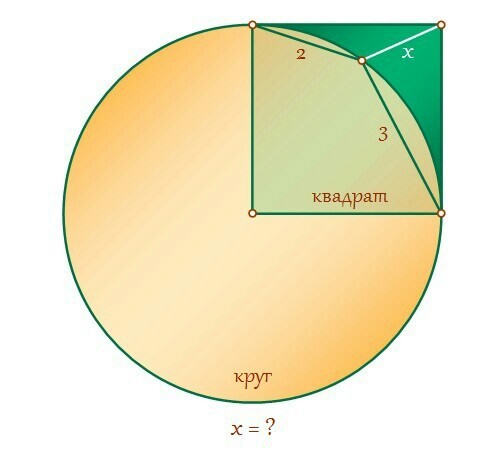
Из центра окружности проведём дополнительный радиус.
Теорема косинусов для двух равнобедренных треугольников с основаниями 2 и 3
2² = 2R² - 2R²cos(β)
3² = 2R² - 2R²cos(90° - β)
---
4 = 2R²(1 - cos(β))
9 = 2R²(1 - sin(β))
---
разделим первое на второе
4/9 = (1 - cos(β))/(1 - sin(β))
4 - 4sin(β) = 9 - 9cos(β)
9cos(β) - 5 = 4sin(β)
---
подстановка
cos(β) = t
sin(β) = √(1-t²)
9t - 5 = 4√(1-t²)
Возводим в квадрат
81t² - 90t + 25 = 16 - 16t²
97t² - 90t + 9 = 0
Дискриминант
D = 90² - 4*97*9 = 4608 = 48²*2
t₁ = (90 - 48√2)/(2*97) = 45/97 - 24√2/97
t₂ = (90 + 48√2)/(2*97) = 45/97 + 24√2/97
---
Радиус окружности (он же сторона квадрата)
4 = 2R²(1 - cos(β))
2 = R₁²(1 - t₁)
R₁² = 2/(1 - t₁) = 2*97/(97 - 45 + 24√2) = 97/(26 + 12√2)
R₁ ≈ 1.50245 - слишком мало, точка пересечения отрезков 2 и 3 за пределами квадрата, отбрасываем это решение
R₂² = 2/(1 - t₂) = 2*97/(97 - 45 - 24√2) = 97/(26 - 12√2)
R₂ ≈ 3.2776 - уже лучше :)
cos(β) = 45/97 + 24√2/97
---
избавимся от иррациональности в знаменателе
R² = 97/(26 - 12√2)
Умножим на (26 + 12√2)
R² = 97*(26 + 12√2)/(26² - 12²*2) = 97*(26 + 12√2)/388 = (13 + 6√2)/2
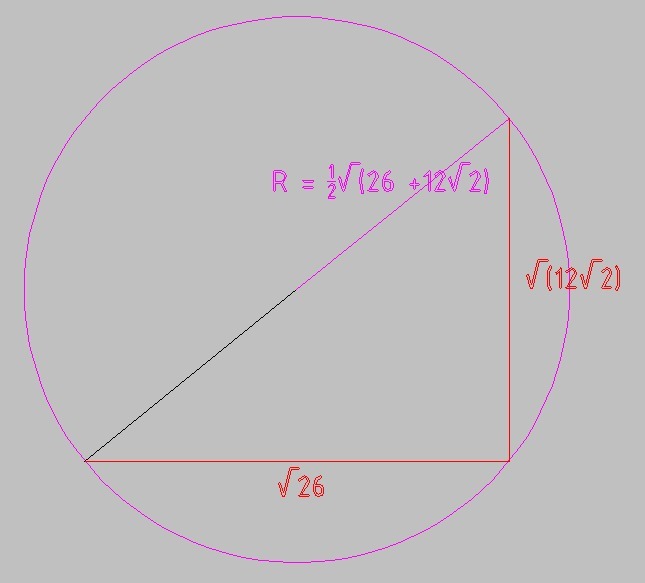
R = √(13/2 + 3√2)
cos(β) = 45/97 + 24√2/97
Для построения этого достаточно :)
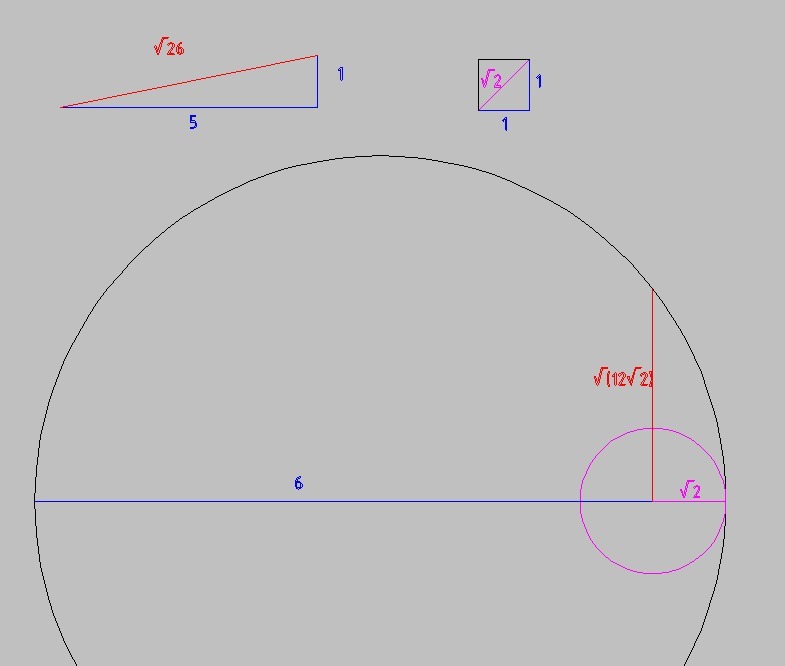
R = 1/2√(26 + 12√2)
1. 26 = 5² + 1², т.е. √26 - это диагональ прямоугольного треугольника с катетами 5 и 1
2. 12√2
отрезок 12, на его конце радиусом √2 (взять из диагонали квадрата со стороной 1), и перпендикулярно строим среднее геометрическое 12 и √2
Оно равно √(12√2)
3. Сложить отрезки пунктов 2 и 1, поделить пополам.
------------------
Величина x получилась равна R₁ ≈ 1.50245