Зробіть і відправте фото
Приложения:
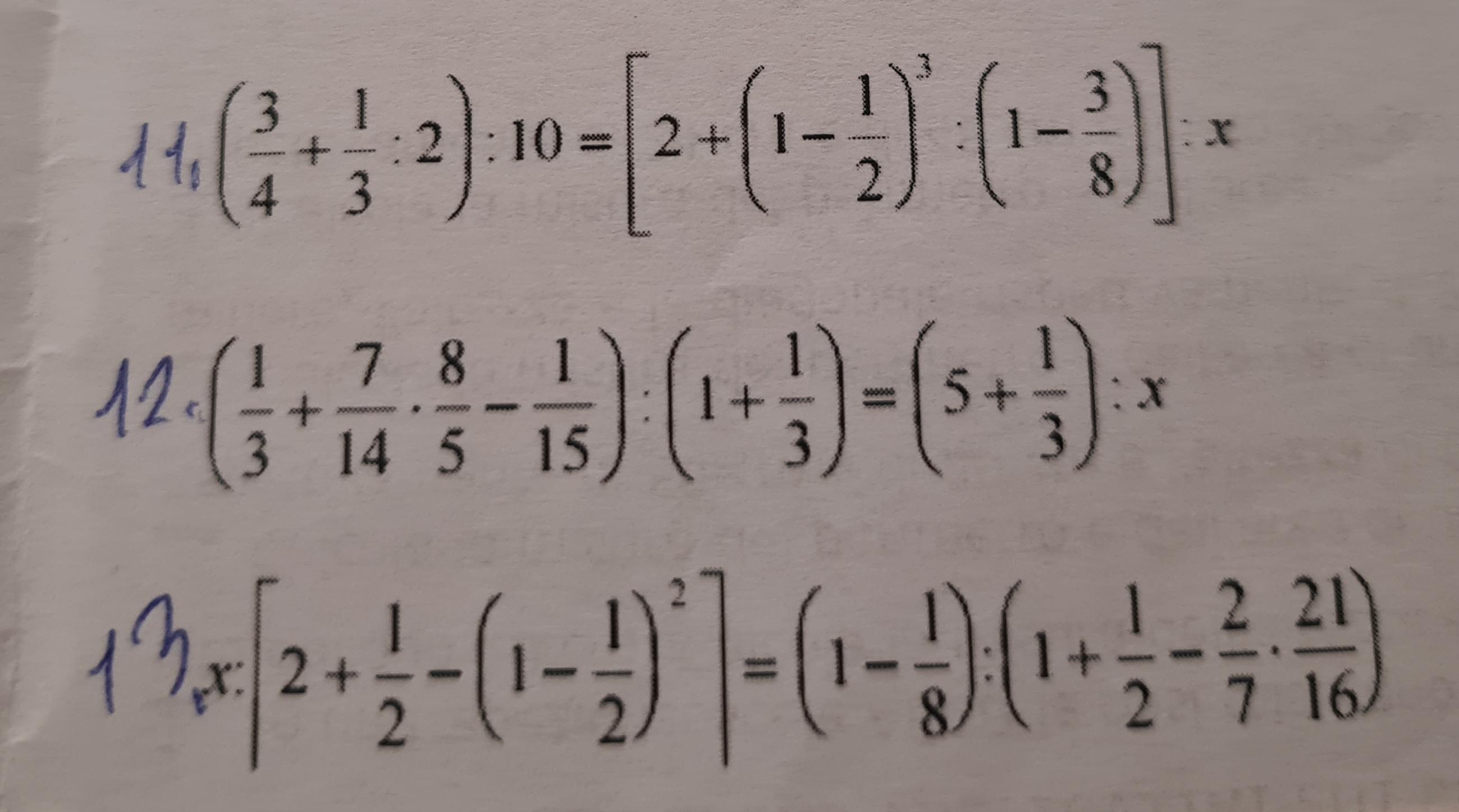
Ответы на вопрос
Ответил NNNLLL54
1
Ответ:
Упростим выражения в правой и левой частях равенства .
Приложения:

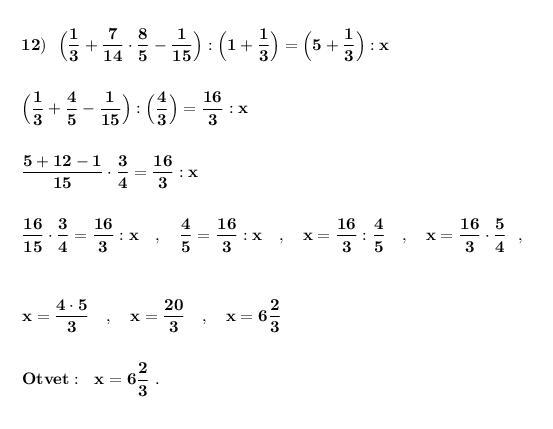

Новые вопросы
Українська мова,
11 месяцев назад
Английский язык,
11 месяцев назад
Математика,
1 год назад
Қазақ тiлi,
1 год назад
Математика,
6 лет назад