Алгебра, вопрос задал kurisenkot44 , 1 год назад

Зробіть добре завдання 50 балів

Приложения:

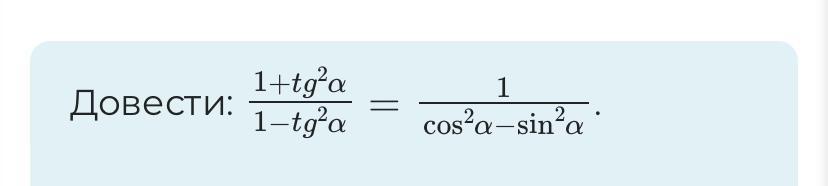
Ответы на вопрос

Ответил Universalka

1

$\displaystyle\bf\\\frac{1+tg^{2}\alpha }{1-tg^{2} \alpha } =\frac{1+\frac{Sin^{2}\alpha }{Cos^{2} \alpha } }{1-\frac{Sin^{2}\alpha }{Cos^{2}\alpha } } =\frac{\frac{Cos^{2} \alpha +Sin^{2} \alpha }{Cos^{2} \alpha } }{\frac{Cos^{2} \alpha -Sin^{2} \alpha }{Cos^{2} \alpha } } =\frac{\frac{1 }{Cos^{2} \alpha } }{\frac{Cos^{2} \alpha -Sin^{2} \alpha }{Cos^{2} \alpha } } =\\\\\\=\frac{Cos^{2} \alpha }{Cos^{2} \alpha \cdot(Cos^{2} \alpha -Sin^{2}\alpha ) } =\frac{1}{Cos^{2} \alpha -Sin^{2} \alpha }$

$\displaystyle\bf\\\frac{1}{Cos^{2} \alpha -Sin^{2} \alpha } =\frac{1}{Cos^{2} \alpha -Sin^{2} \alpha }$

Что и требовалось доказать .

sdhjfsdhjfsdhjfhj: Универсалка, добрый день, не могли бы Вы помочь с алгеброй? https://znanija.com/task/51065287

sdhjfsdhjfsdhjfhj: Задание находится в профиле

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Немецкий язык, 1 год назад

Поставте слова у правильному порядку, щоб утворилися речення 1. hat, gut, Erikas, gefeiert, Familie, Ostern. 2. Geschichte, dir, kann, interessante, erzählen, ich, eine. 3. ein Stadion, in, viele,...

История, 1 год назад

Складіть мініпортфоліо за матеріалами параграфа (тобто використовуємо інформацію лише з параграфа) на таких історичних діячів: К. Левицький, А. Волошин, Ю. Романчук, І. Боберський, К. Трильовський...

Английский язык, 1 год назад

Помогите срочно англ пожалуйста...

Русский язык, 1 год назад

Комментированное письмо Сказка - [c] - сказать - Ко...ьба - - Оши...ка Моро...- Сне...- Варе...ка- Сторо...ка -- - оглушение...

Другие предметы, 6 лет назад

СРОЧНОО!! Составить таблицу с обитателями почвы и способами их приспособления к жизни в почвенной среде (минимум 7 животных)...

Алгебра, 6 лет назад

2) y =1/3x+2, -3≤х≤3 скажите пожалуйста ответ срочно нужно,и не в крации, а точно...