зовнішній кут трикутника у 2 рази більший за один з внутрішніх кутів не суміжний з ним. доведіть що трикутник рівнобедрений​

Ответ:

Объяснение:

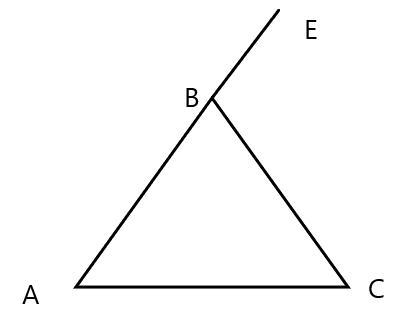
Дано: Δ АВС

∠ЕВС=2∠ВАС

Довести: ΔАВС- рівнобедрений (∠ВАС=∠ВСА)

Розв'язання:

Нехай ∠ВАС =х, тоді ∠ЕВС=2х (за умовою).

∠ЕВС та ∠АВС- суміжні⇒ ∠ЕВС+∠АВС =180°

∠АВС =180°-∠ЕВС= 180°-2х

∠ВАС+∠АВС+∠ВСА=180° ⇒

∠ВСА= 180° -∠ВАС-∠АВС= 180° -х-(180°-2х)=180°-х-180°+2х=-х+2х=х⇒

∠ВАС=∠ВАС ⇒ΔАВС - рівнобедрений, з основою АС

або

Нехай ∠ВАС =х, тоді ∠ЕВС=2х (за умовою).

За властивістю зовнішнього кута, зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних із ним, тобто

∠ЕВС = ∠ВАС+∠ВСА ⇒ ∠ВСА=∠ЕВС-∠ВАС= 2х-х=х

Маємо ∠ВСА=∠ВАС ⇒ ΔАВС - рівнобедрений, з основою АС