Алгебра, вопрос задал lenafffkoror , 6 месяцев назад

Знайти значення параметра k

Приложения:

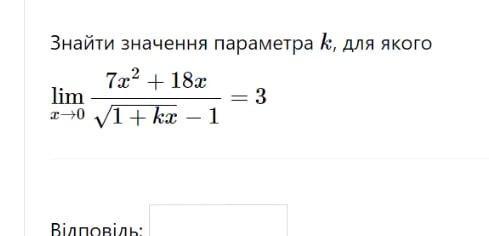
Ответы на вопрос

Ответил axatar
0

Ответ:

Если \tt \displaystyle \lim_{x\rightarrow 0} \frac{7 \cdot x^2+18 \cdot x}{\sqrt{1+k \cdot x} -1} =3, то k = 12

Объяснение:

Требуется найти значение параметра k, если

\tt \displaystyle \lim_{x\rightarrow 0} \frac{7 \cdot x^2+18 \cdot x}{\sqrt{1+k \cdot x} -1} =3.

Решение. Избавимся от иррациональности в знаменателе и упростим:

\tt \displaystyle \lim_{x\rightarrow 0} \frac{7 \cdot x^2+18 \cdot x}{\sqrt{1+k \cdot x} -1} =\lim_{x\rightarrow 0} \frac{(7 \cdot x^2+18 \cdot x) \cdot (\sqrt{1+k \cdot x} +1)}{(\sqrt{1+k \cdot x} -1) \cdot (\sqrt{1+k \cdot x} +1) } = \\\\ =\lim_{x\rightarrow 0} \frac{(7 \cdot x+18) \cdot x \cdot (\sqrt{1+k \cdot x} +1)}{(\sqrt{1+k \cdot x})^2 -1^2 } =\lim_{x\rightarrow 0} \frac{(7 \cdot x+18) \cdot x \cdot (\sqrt{1+k \cdot x} +1)}{1+k \cdot x -1 } =

\tt \displaystyle =\lim_{x\rightarrow 0} \frac{(7 \cdot x+18) \cdot x \cdot (\sqrt{1+k \cdot x} +1)}{k \cdot x } =\lim_{x\rightarrow 0} \frac{(7 \cdot x+18) \cdot (\sqrt{1+k \cdot x} +1)}{k} = \\\\ = \frac{(7 \cdot 0+18) \cdot (\sqrt{1+k \cdot 0} +1)}{k} =\frac{18 \cdot 2}{k} =\frac{36}{k} =3

Отсюда

3·k = 36 или k = 12.

#SPJ1

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Физика, 4 месяца назад
пожалуйста срочно 6. Сколько молей газообразного ацетилена (C2H2) имеет массу 39 г (Мс н2 = 0,026-)? моль A) 0,065 B) 1.5 C) 0,65 D)0,013 E) 0,5 истанаICH​...
Биология, 4 месяца назад
Низшие растения конспект...
Геометрия, 6 месяцев назад
Знайдіть невідомі сторони й кути трикутника АВС, якщо АВ=14, <A=64°, ∠B = 48°.​
Химия, 6 месяцев назад
ХІМІЯ допоможіть будь ласка 1. Чи показують структурні формули загальну кількість атомів в молекулі? Поясніть на прикладах. 2. Чи вірне наступне судження: «Причиною гібридизації є утворення...
Литература, 6 лет назад
Над чем смеётся и что гневно обсуждает Гоголь в поэме Мёртвые души...
Математика, 6 лет назад
Помогите с заданием к подготовке к экзамену...