Знайти всі значення а за яких рівняння має один корінь
Приложения:
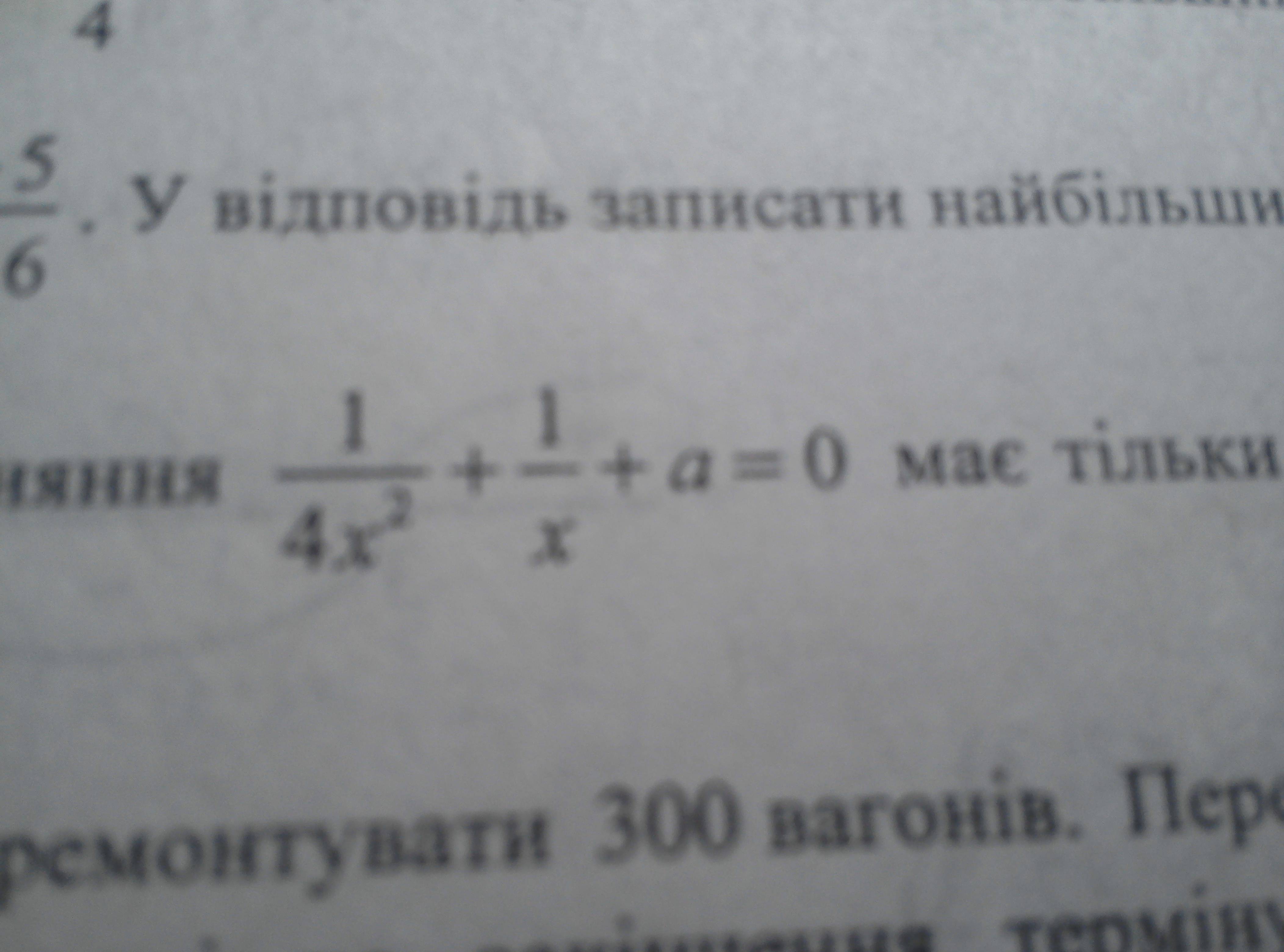
Ответы на вопрос
Ответил maksimcat
0
1)рассмотрим случай, когда дискриминант равен нулю
D=16-16a=16(1-a)
при а=1 уравнение имеет один корень х=-1/2
2) рассмотрим случай, когда дискриминант не равен нулю , один из корней равен 0
1-а>0;a<1
при а=1 уравнение имеет один корень х=-1/2
при а=0 уравнение имеет один корень х=-1/4
Ответил Аноним
0
Умножим левую и правую части уравнения на , получим
Квадратное уравнение имеет единственный корень, если дискриминант равно нулю:
Также заметим, что если коэффициент при старшем степени х, равняется нулю, то есть откуда
то уравнение примет линейный вид, что имеет один корень х= -0,25.
ОТВЕТ: -0,25 и 1.
Новые вопросы