Знайти та зобразити область визначення функції декількох змінних;
z=1+√(x-y)^3
Ответы на вопрос
Ответил mishsvyat
1
Ответ:
Т.к. в функции присутствует квадратный корень, то следует записать для него ОДЗ:
Таким образом, нужно решить неравенство. Заметим, что:
Для второго множителя неравенство выполняется при любых значениях x и y . Значит можно ограничиться первым множителем:
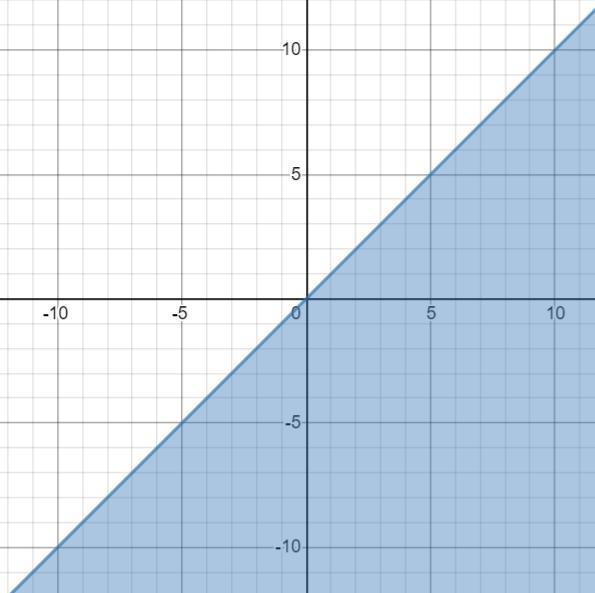
Таким образом, область определения функции - область, лежащая на и под графиком функции
Приложения:
Ответил NNNLLL54
1
Ответ:
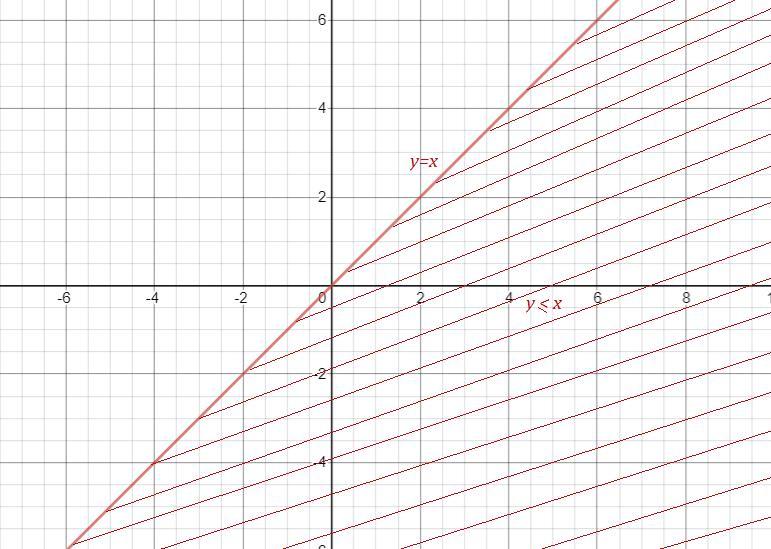
Областью определения функции двух переменных будет часть плоскости, лежащая ниже прямой у=х , причём граница области, сама прямая у=х , входит в эту область .
Приложения:
Новые вопросы