Алгебра, вопрос задал Katrin333337 , 9 лет назад

знайти похідну функції

Приложения:

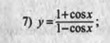
Ответы на вопрос

Ответил nafanya2014

$y=(( sqrt{x} -2)(5-6 sqrt{x} ))`= \ \ =( sqrt{x} -2)`cdot(5-6 sqrt{x} )+( sqrt{x} -2)cdot (5-6 sqrt{x} )`= \ \ = frac{1}{2 sqrt{x} }cdot (5-6 sqrt{x} )+( sqrt{x} -2)cdot (-6cdotfrac{1}{2 sqrt{x} })= \ \ =frac{1}{2 sqrt{x} }cdot (5-6 sqrt{x} -6 sqrt{x} +12)=frac{1}{2 sqrt{x} }(17-12 sqrt{x} )$

$y`=( frac{1+cosx}{1-cosx})`= frac{(1+cosx)`(1-cosx)-(1+cosx)(1-cosx)`}{(1-cosx) ^{2} }= \ \ =frac{(-sinx)(1-cosx)-(1+cosx)(sinx)}{(1-cosx) ^{2} }=frac{-sinx+sinxcdot cosx-sinx-sinxcdot cosx}{(1-cosx) ^{2} }= \ \ = frac{-2sinx}{(1-cosx) ^{2} }$

Ответил kazimierz2015

$y=( sqrt{x}-2)(5-6 sqrt{x}) \ y'= frac{1}{2 sqrt{x} }(5-6 sqrt{x})-3 sqrt{x}( sqrt{x}-2)= frac{5-6 sqrt{x} }{2 sqrt{x} } -3x+6 sqrt{x} \ y= frac{1+cosx}{1-sinx} \ y'= frac{-sinx(1-sinx)+cosx(1+cosx)}{cos^2x}= frac{-sinx+sin^2x+cosx+cos^2x}{cos^2x} \ y'= frac{1-sinx+cosx}{cos^2x} \$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 2 года назад

Помогите написать рассказ на английском языке ! write a short biography of this person 60-80 words. Нужно написать либо про Николая Баскова либо про Филиппа Киркорова...

Қазақ тiлi, 2 года назад

вопросы Бір адам жас баласын жанына алды. Екеуі сайран етіп кетіп қалды Кыдырып әрлі-берлі нурлi дагы Егінші егін екен жерге барды Аралап әр егінді қарап жүрді, Кез едi nicin болған егін түрлі...

Алгебра, 9 лет назад

упростить выражение; 5b в кубе -(а в квадрате +5b)×(ab-b в квадрате"...

Алгебра, 9 лет назад

Очень надо!Решите пожалуйста,я уже ничего не понимаю 1) (х+2)(х-2)-х(х-6)=0 2) -4х+5=-9х-20...

Литература, 9 лет назад

кто такая классная дама...

Геометрия, 9 лет назад

Помогите решить задачу по геометрии!на рис.2 <ВАЕ=112 градусов.,<ДВF=68 градусов,AC=9 см.Найдите сторону АС в треугольнике АВС...