Знайти площу рівнобічної трапеції, у якої основи 6 см і 10 см, а діагоналі взаємно пенпердикулярні​

Відповідь:

S = 64 см²

Пояснення:

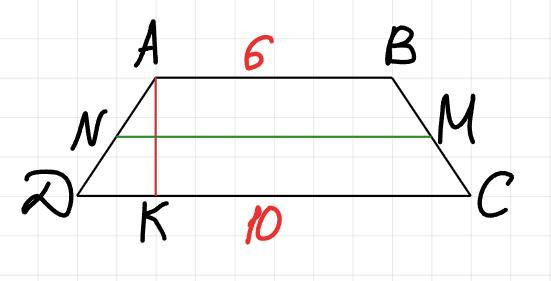
З властивостей рівнобедреної трапеції відомо, що якщо її діагоналі перпендикулярні, то її висота дорівнюватиме півсумі основ. Середня лінія трапеції також дорівнює півсумі основ. То ж NM = AK, де NM - середня лінія трапеції, а AK - висота трапеції.

Знайдемо середню лінію трапеції:

(см)

Знайдемо площу трапеції:

(см²)