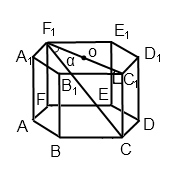
Знайти об єм правильної шестикутної призми, в якій більша діагональ дорівнює l і утворює з площиною основи кут а.
Ответы на вопрос
Объем призмы находится по формуле: V = S * h, где S - площадь основания, h - высота призмы.
Для того, чтобы найти площадь правильного шестиугольника, нужно найти его сторону.
Сторона шестиугольника равна радиусу его описанной окружности.
Треугольник F1C1C - прямоугольный => cos α = F1C1 / F1C
cos α = F1C1 / l
F1C1 = l * cos α
F1C1 - диаметр описанной окружности. R = OC1 = (l * cos α) / 2
Соединив точку О со всеми вершинами шестиугольника A1B1C1D1E1F1 мы получим шесть равных равносторонних треугольников.
Значит площадь шестиугольника равна шести площадям этих треугольников.
Площадь треугольника находим по следующей формуле:
S = 0,5 * a * b * sin α, где α - угол между сторонами a и b.
Так как мы находим площадь равностороннего треугольника α будет равен 60°.
S BOC1 = 0,5 * ((l * cos α) / 2) * ((l * cos α) / 2) * sin 60° = 0,5 ((l ² * cos ² α) / 4) * (√3) / 2 = ((√3) * l ² * cos ² α) / 16.
S A1B1C1D1E1F1 = S BOC1 * 6 = (( (√3) * l ² * cos ² α) / 16) * 6 = (3 * (√3) * l ² * cos ² α) / 8.
Высоту CC1 можно вычислить из треугольника F1C1C - sin α = C1C / F1C
sin α = C1C / l
C1C = l * sin α
V = ((3 * (√3) * l ² * cos ² α) / 8) * (l * sin α) = (3 * (√3) * l ³ * cos ² α * sin α) / 8.