Знайти границі послідовності.
Приложения:
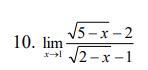
Ответы на вопрос
Ответил 7x8
1
Ответ:
Объяснение:
fctdgsygfdhngfxzgsac:
дуже дякую)
Ответил NNNLLL54
2
Ответ:
Неопределённость вида 0/0 . Домножаем на сопряжённые выражения , чтобы воспользоваться формулой разности квадратов (а-b)(а+b)=a²-b² .
Приложения:
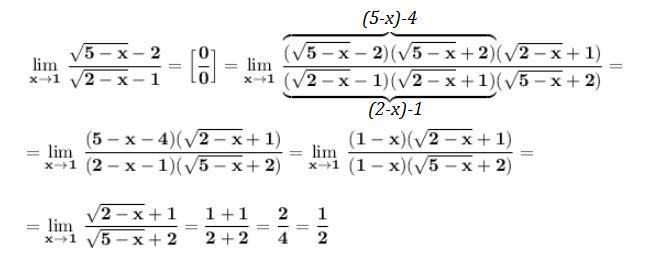
здравствуйте, помогите пожалуйста решить задачу
Новые вопросы
Українська мова,
11 месяцев назад
История,
11 месяцев назад
Английский язык,
11 месяцев назад
Алгебра,
11 месяцев назад
Русский язык,
6 лет назад