Знайдіть вершину параболи і точки перетину графіка функції
Приложения:
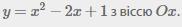
Ответы на вопрос
Ответил mishsvyat
0
Ответ:
Координаты вершины: (1;0)
Точка пересечения с осью X: (1;0)
Объяснение:
Общий вид уравнения параболы:
Координаты вершины:
Точки пересечения с осью Х определяются из решения квадратного уравнения:
Подставляя заданную функцию, получим:
Решая квадратное уравнение, получим:
Парабола пересекает ось Х в вершине
Ответил matilda17562
0
Ответ:
(1;0)
Объяснение:
1. хo = -b/(2a) = -(-2)/(2•1) = 2/2= 1;
yo = y(1) = 1^2 - 2•1 + 1 = 0
(1;0) - координаты вершины параболы.
2. Так как ветви параболы направлены вверх (а=1, 1 > 0), и вершина параболы лежит на оси Ох, то других точек пересечения с осью Ох нет.
Если это хочется показать по-другому, то решение может быть таким:
у = 0, тогда
х^2 - 2х + 1 = 0
(х - 1)^2 = 0
х - 1 = 0
х = 1
(1;0) - единственная точка пересечения параболы с осью Ох.
Новые вопросы