Знайдіть проміжки монотонності функцій: (на фото)
Приложения:

Ответы на вопрос
Ответил lvv9136
1
Ответ:
см фото
Пошаговое объяснение:
Приложения:
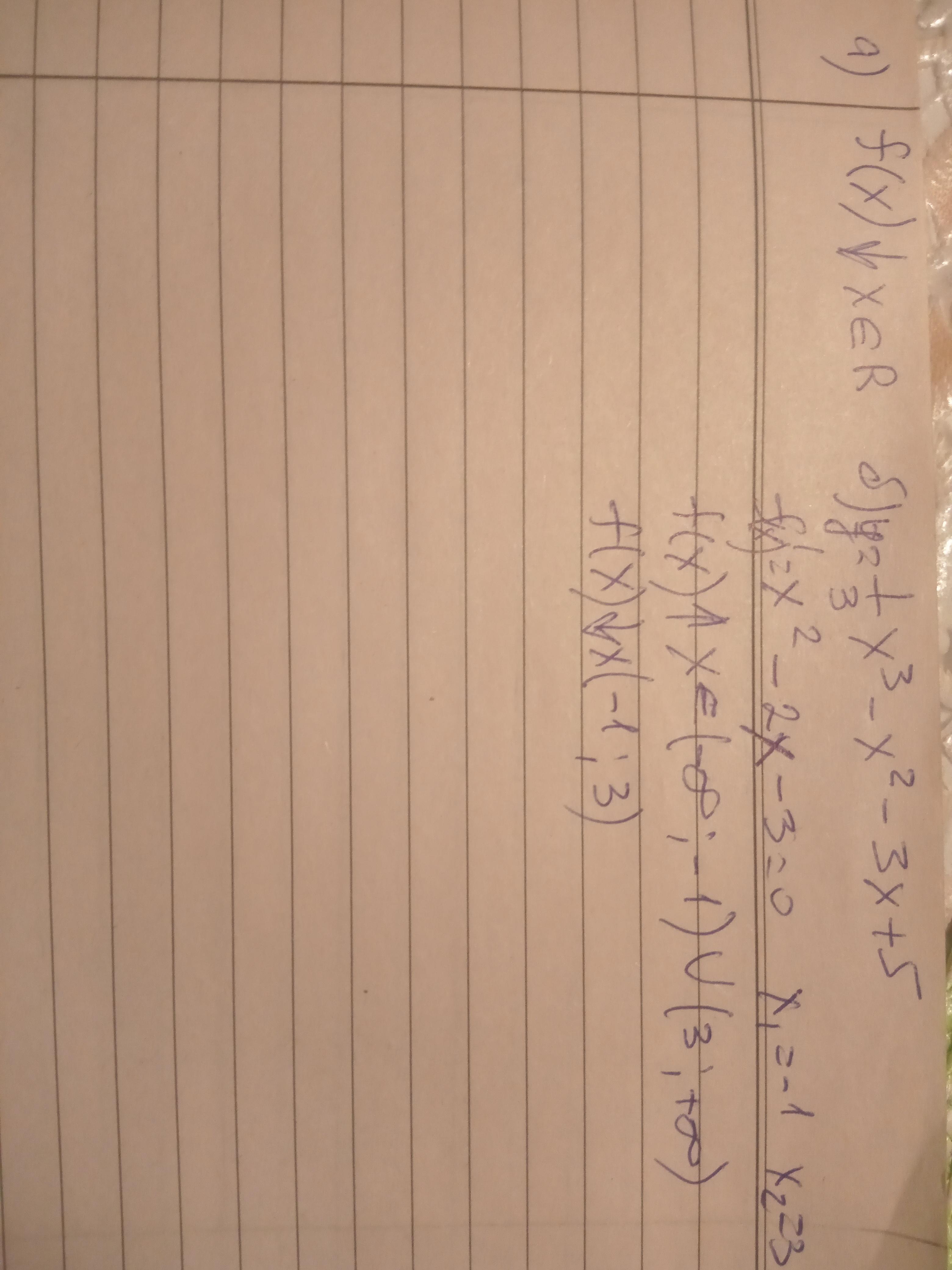
Ответил balakine977
1
Ответ:
а) убывает на R
б) промежуток возрастания f(x): (-∞; -1] ∪ [3; +∞), промежуток убывания f(x): [-1; 3]
Пошаговое объяснение:
а) f(x) - линейная функция, она монотонна (убывает, так как коэффициент при x меньше нуля) на всей числовой прямой.
б) Функция монотонна в тех промежутках, в которых её производная имеет постоянный знак (причём если знак +, то ф-я возрастает, а если знак -, то убывает).
Найдём, при каких значениях x :
или
Итак, при x > 3 или x < -1. При других значениях x, соответственно,
.
Значит, промежуток возрастания f(x): (-∞; -1] ∪ [3; +∞)
Соответственно, промежуток убывания f(x): [-1; 3]
Новые вопросы