Знайдіть похідну функції f(x)=(√x-2)(5-6√x)
Приложения:
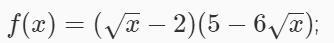
Ответы на вопрос
Ответил liftec74
0
Ответ: =(8.5-6√x)/√x
Объяснение:
f'(x)= u'(x)*v(x)+ u(x)*v'(x)
u(x)=(√x -2) v(x)=5-6√x
u'(x)=0.5* 1/√x v'(x)=-6*0.5/√x = -3/√x
=
Новые вопросы