Знайдіть похідну 100
Приложения:
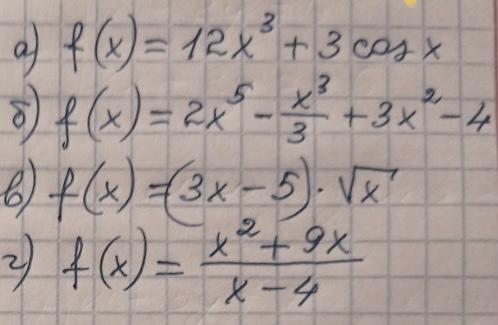
Ответы на вопрос
Ответил Аноним
2
(xⁿ)'=n*xⁿ⁻¹
(uv)'=u'v+uv'
(u/v)'=(u'v-uv')/v²
(√x)'=1/(2√x)
(cosx)'=sinx
a) f'(x)=3*12x²-3sinx=36x²-3sinx
б) f'(x)=10x⁴-3x²/3+6x-0=10x⁴-x²+6x
в) f'(x)=(3x-5)'*√x+(3x-5)*(√x)'=3√x+(3x-5)/(2√x)=(6x+3x-5)/(2√x)=
(9x-5)/(2√x)
г) f'(x)=((2x+9)*(x-4)-1*(x²+9x))/(x-4)²=(2x²+9x-8x-36-x²-9x)/(x-4)²=
(x²-8x-36)/(x-4)²=
daniakucher292:
Дякую:)
Ответил NNNLLL54
1
Ответ:
Используем правила дифференцирования:
.
Помогите пожалуйста вычислить определенный интеграл, не могу ни как сделать
Новые вопросы
Английский язык,
1 год назад
Английский язык,
6 лет назад
Математика,
6 лет назад
Математика,
8 лет назад
Математика,
8 лет назад