Математика, вопрос задал katay502 , 6 лет назад

знайдіть похідні функції

Приложения:

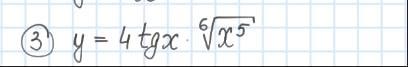
Ответы на вопрос

Ответил MatemaT123

1

Ответ:

$\dfrac{4\sqrt[6]{x^{5}}}{\cos^{2}x}+\dfrac{10tgx}{3\sqrt[6]{x}}$

Пошаговое объяснение:

$y=4tgx \cdot \sqrt[6]{x^{5}}=4tgx \cdot x^{\tfrac{5}{6}};$

$y'=(4tgx \cdot x^{\tfrac{5}{6}})'=(4tgx)' \cdot x^{\tfrac{5}{6}}+4tgx \cdot (x^{\tfrac{5}{6}})'=4 \cdot (tgx)' \cdot \sqrt[6]{x^{5}}+4tgx \cdot \dfrac{5}{6} \cdot x^{\tfrac{5}{6}-1}=$

$=\dfrac{4\sqrt[6]{x^{5}}}{\cos^{2}x}+\dfrac{20}{6}tgx \cdot x^{-\tfrac{1}{6}}=\dfrac{4\sqrt[6]{x^{5}}}{\cos^{2}x}+\dfrac{10tgx}{3} \cdot \bigg (\dfrac{1}{x} \bigg )^{\tfrac{1}{6}}=\dfrac{4\sqrt[6]{x^{5}}}{\cos^{2}x}+\dfrac{10tgx}{3} \cdot \sqrt[6]{\dfrac{1}{x}}=$

$=\dfrac{4\sqrt[6]{x^{5}}}{\cos^{2}x}+\dfrac{10tgx}{3\sqrt[6]{x}};$

katay502: спасибо большое

MatemaT123: Пожалуйста.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Написать 10-15 вопросов с IS, ARE, AM. И ответы на эти вопросы,хотя бы 5~6 для 3 класса не сложные...

Русский язык, 1 год назад

составит славосачитание с даными словами ножницы цыганский цыферблат птенцы цыркуль цынк пунктуацыя артикуляцыя цыплёнок тенденцыя цывилизацыя энцыклопедия мудрецы систрицына...

Геометрия, 6 лет назад

будь ласка виконайте завдання на фото,через "Дано"...

Математика, 6 лет назад

$36 \div ( - \frac{4}{13} )$ срочно буду очень блогодарен ...

Химия, 8 лет назад

Как получить из 2-хлорпропана 2,3-диметилбутан, а потом углекислый газ?

Биология, 8 лет назад

8 пословиц либо поговорок о хвойных растениях. Заранее спасибо. 15 баллов.