Математика, вопрос задал anastasia94555 , 2 года назад

знайдіть площу фігури обмеженої лініями y=-4/x y=5+x

Ответы на вопрос

Ответил mionkaf1

2

$y=-\frac{4}{x}##\\y=5+x$

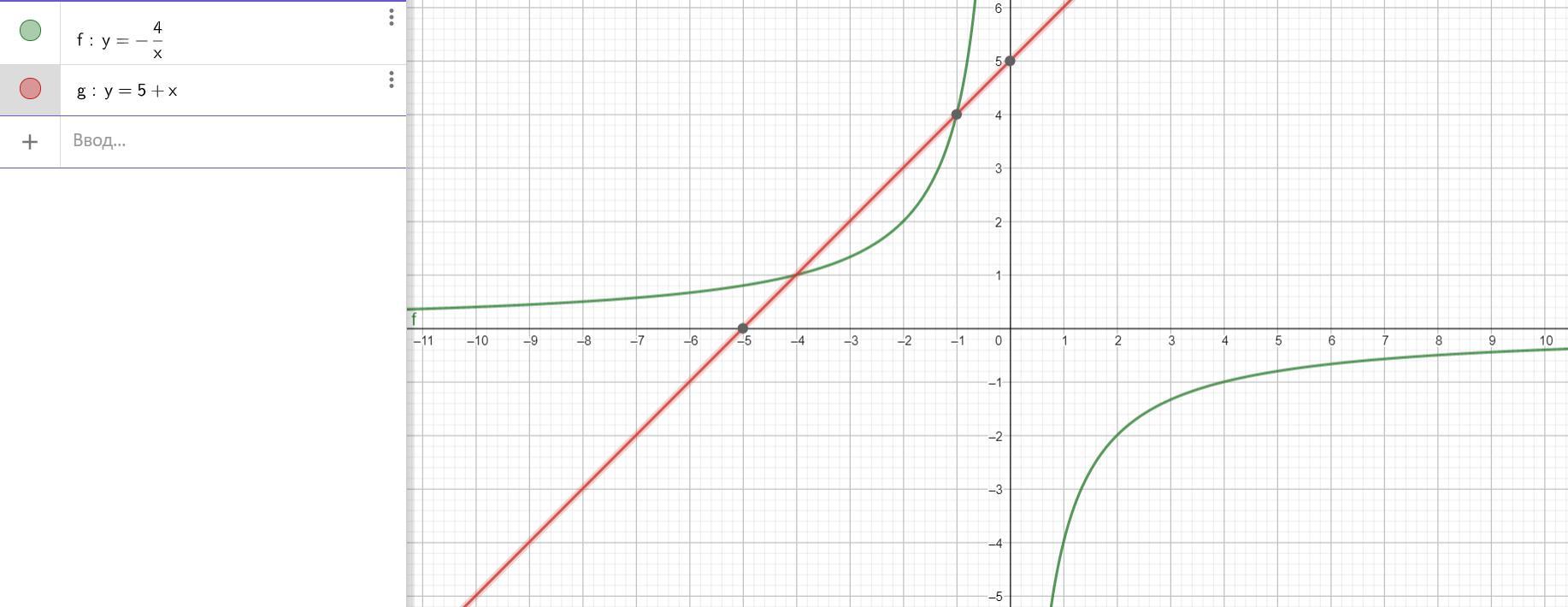
См. рис.

Точки пересечения графиков : x₁=-4,x₂=-1

$S=\int^{-1}_{-4}(5+x-(-\frac{4}{x}))dx=(5x+\frac{x^2}{2}+4*ln(\mid x \mid))\mid^{-1}_{-4}=\\\\=5*(-1)+\frac{(-1)^2}{2}+4*ln\mid-1\mid-(5*(-4)+\frac{(-4)^2}{2}+4*ln\mid 4 \mid)=\\\\=-5+\frac{1}{2}+4*0-(-20+8+4*ln(4))=-5+\frac{1}{2}+12-4ln(4)=\frac{15}{2}-4ln(4)$

Ответ: $\frac{15}{2}-4ln(4)$ ед²

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

хотя бы на этот помогите ответить а не молчитеее(((!!!((((...

Русский язык, 1 год назад

Проверьте мой тест по русскому и исправьте ошибки Пожалуйста, завтра сдавать.

Английский язык, 2 года назад

1. Поставь прилагательное в нужную форму и переведи предложения. 1. This book is the ………..book ever! interesting 2. He is ……….at playing the violin than his brother. good 3. Mary is ……….than...

Английский язык, 2 года назад

Помогите пожалуйста...

ОБЖ, 7 лет назад

Меры предосторожности по защите населения Доклад...

Геометрия, 7 лет назад

помогите пожалуйста, срочно...