Знайдіть первісну функції /(х) = 49-2х +3, графік якої проходить через точку А (1; -2).
NNNLLL54:
f(x) = ?
49-2x+3=52-2x ...
Ответы на вопрос
Ответил shadowmarder20
0
Відповідь:
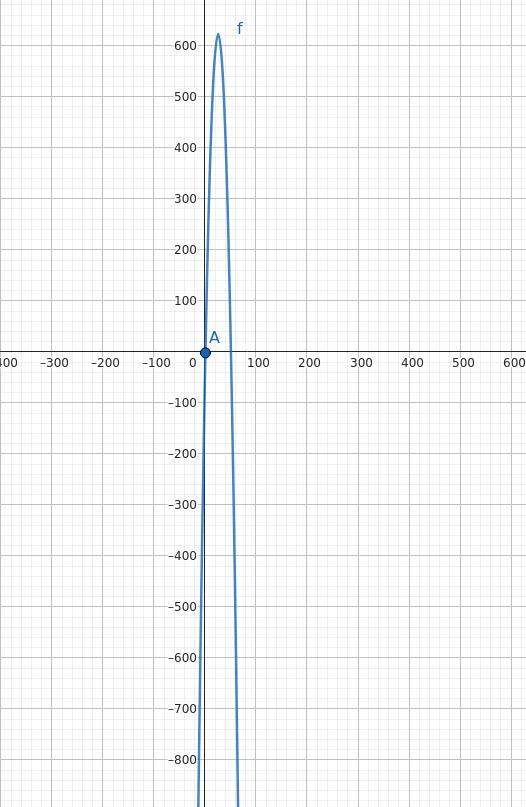
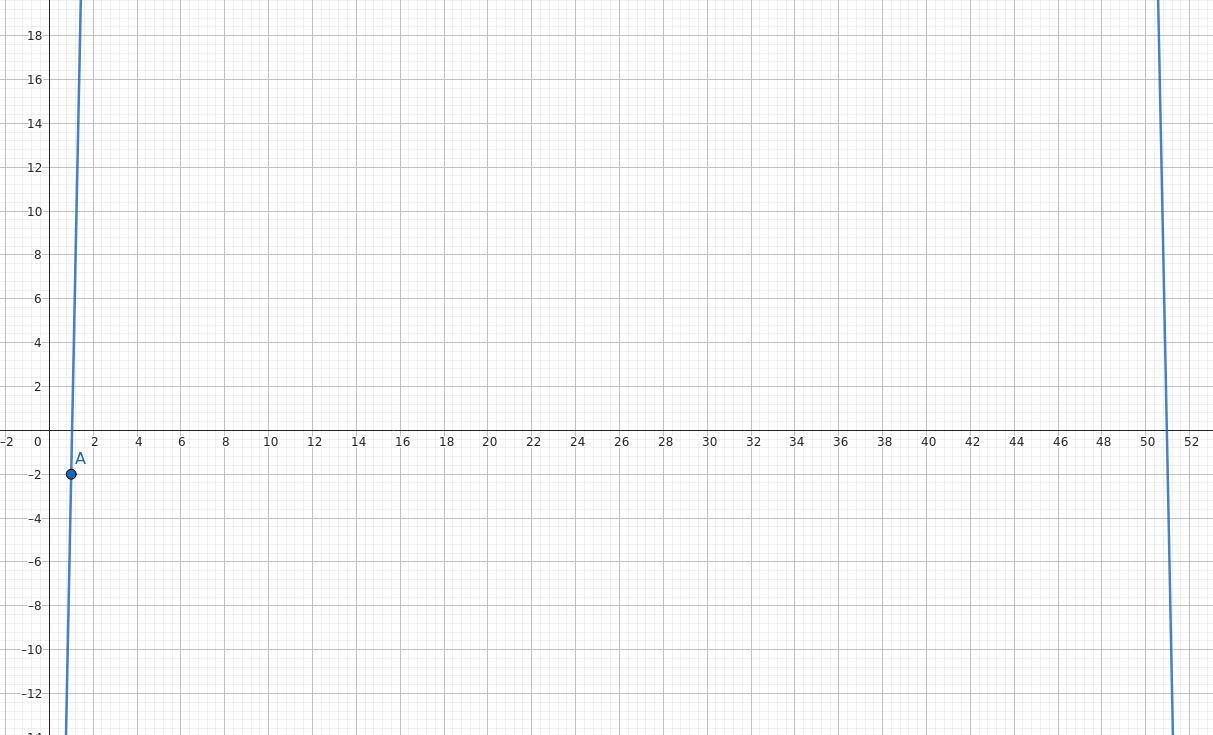
F(x)=52x-x²-53
Пояснення:
f(x) = 49-2x+3 = 52-2x¹
Шукаємопервісну за таблицею:
Тепер ми маємо цю функцію:
y = 52x-x²+C
Нам потрібно знайти таке C, при якому вона буде проходити через точку A(1, -2). Найпростіше це зробити це просто підставити координати точки A(1;-2) в рівняння (замість x один, замість y мінус два):
-2=52*1-1²+C
-2= 52-1+C
-2=51+C
-2-51=C
-53=C
Одже C дорівнює -53 повертаємось до графіка первісної:
F(x)=52x-x²+C Підставляємо C і отримуємо відповідь:
F(x)=52x-x²-53
(Таблиця взята із формул НМТ)
Приложения:

Новые вопросы
Английский язык,
2 месяца назад
История,
2 месяца назад
Другие предметы,
2 месяца назад
География,
2 месяца назад