Знайдіть кути паралелограма, якщо його діагональ перпендикуляр однієї зі сторін і дорівнює половині іншої сторони.
Можно с дано и тд

Відповідь:

∠А =30*; ∠В =150*; ∠С=30*; ∠D=150*

Пояснення:

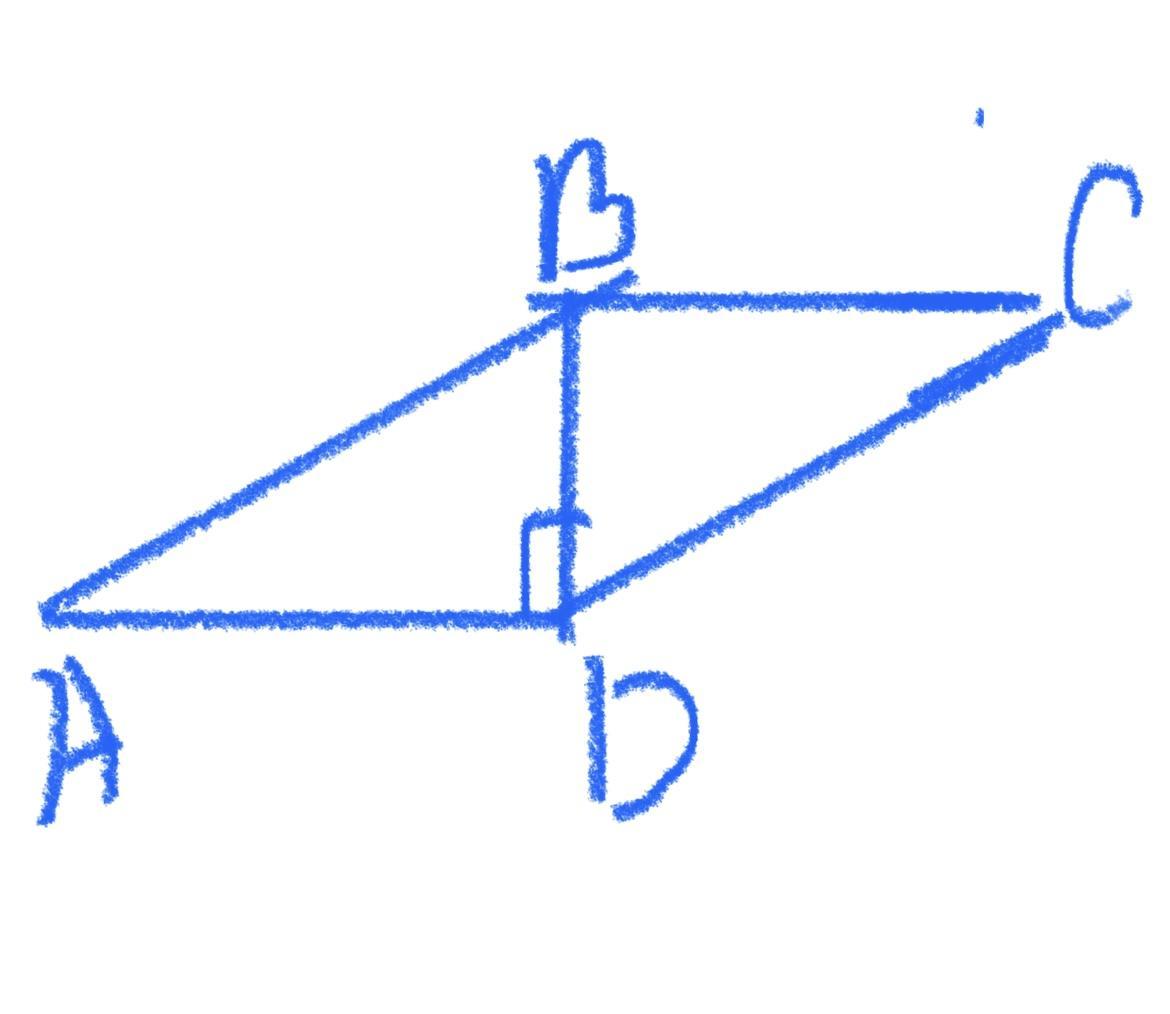
Дано:

АВСD - паралелограм; ВD⊥AD;

BD = 1/2 AB.  
Знайти:

∠А - ?; ∠В - ?; ∠С - ?; ∠D - ?

Розв‘язання:

У прямокутному трикутнику, якщо катет дорівнює половині гіпотезузи, то кут, що лежить напроти цього катета, дорівнює 30*.

Трикутник АВD - прямокутний

( ВD⊥AD), ВD = 1/2AB;

звідси ∠А = 30*. 
Протилежні кути паралелограма рівні: 

∠А =∠С= 30*;∠В =∠D

Сума кутів, прилеглих до однієї сторони становить 180*; ∠А+∠В=180*
звідси:

∠В = 180 - ∠А; 
∠В = 180-30=150* 

∠В = ∠D = 150*. 
 Відповідь:  ∠А =30*; ∠В =150*; ∠С=30*; ∠D=150*