Знайдіть критичні точки функції f(х)=3х^2-х^3. Допоможіть будь ласка
Ответы на вопрос
Ответил ksamohina46
1
Пошаговое объяснение:
Щоб знайти критичні точки функції, необхідно знайти її похідну та розв'язати рівняння f'(x) = 0.
f(x) = 3x^2 - x^3
f'(x) = 6x - 3x^2
Розв'язуємо рівняння f'(x) = 0:
6x - 3x^2 = 0
3x(2 - x) = 0
Таким чином, ми маємо дві критичні точки: x = 0 та x = 2.
Щоб з'ясувати, чи ці точки є максимумами, мінімумами або точками перегину, необхідно дослідити знак похідної f'(x) в околі кожної точки.
Для x < 0, f'(x) < 0, тобто функція спадає.
Для 0 < x < 2, f'(x) > 0, тобто функція зростає.
Для x > 2, f'(x) < 0, тобто функція спадає.
Отже, точка x = 0 є максимумом, а точка x = 2 є мінімумом функції.
Ответил aarr04594
1
Відповідь: 0; 2.
Покрокове пояснення:
розв'язання завдання додаю
Приложения:
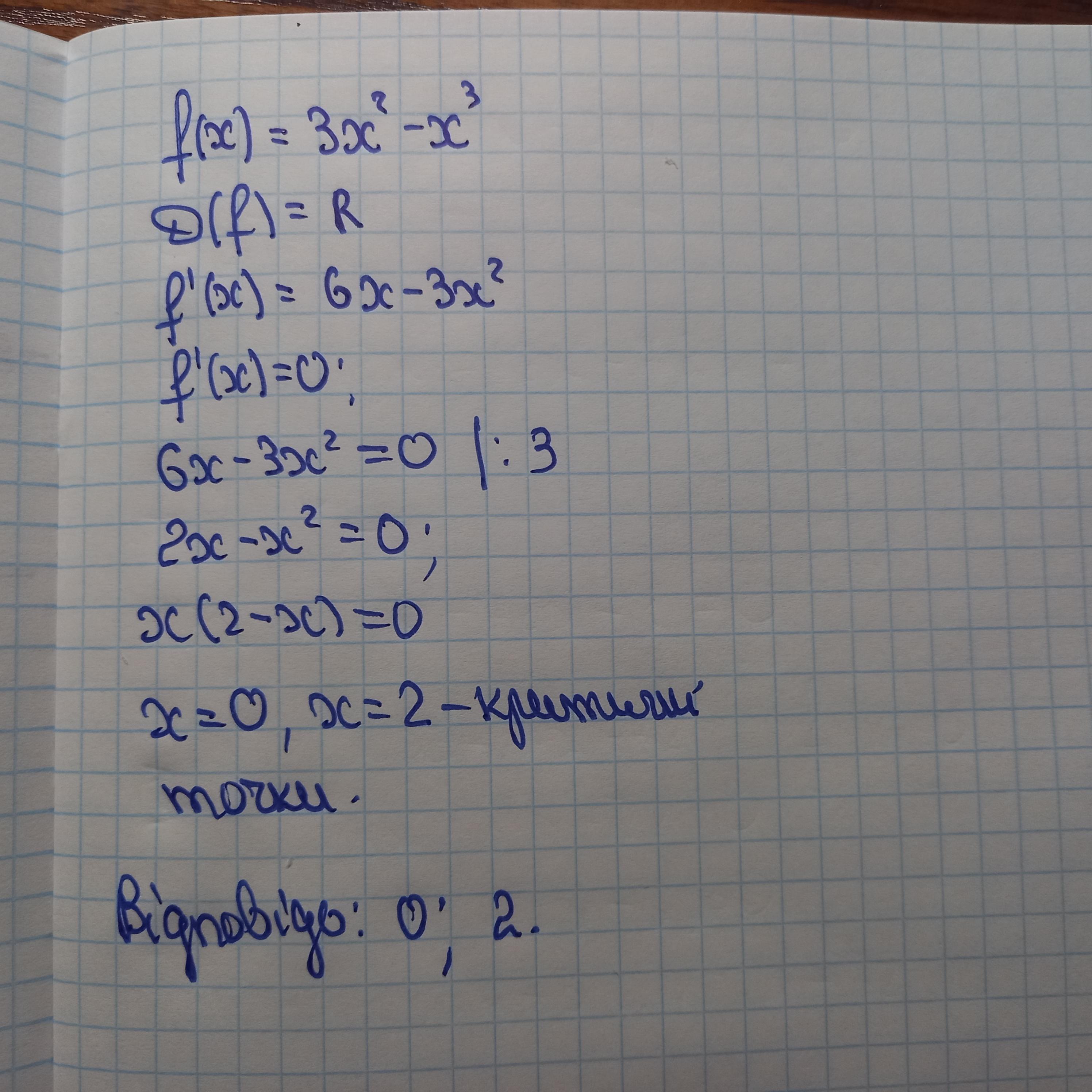

artemmms12:
дякую вам велике, чи можете мені допомогти ще з одним завданням, але я не можу його виставити сюди, чи можу я вам написати кудись?
Тут можете написати? Зі збірника, підручника?
в мене немає дозволу писати(
Тут в коментах можете написати завдання?
Тіло рухається прямолінійно за законом х (t)=2/3 t^3-t^2 Знайдіть його миттєву швидкість і прискорення в момент часу t = 3 с.
Я зараз додам тут. У вас там ще дослідити функцію, теж треба нормальну відповідь?
так, дуже вам дякую
Див. другий файл.
дякую, дуже допомогли мені
Дослідження на сторінці, де ви розміщували функцію, додала.
Новые вопросы
Алгебра,
1 год назад
Литература,
1 год назад
Физика,
1 год назад
Химия,
6 лет назад
Математика,
6 лет назад