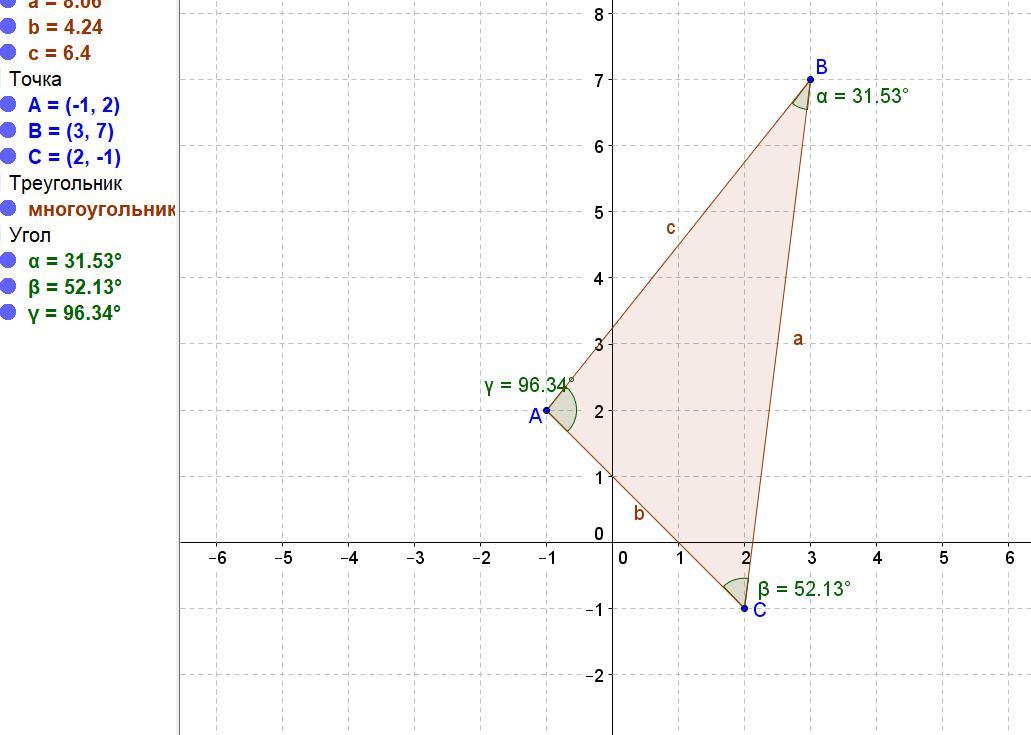
знайдіть косинуси кутів a трикутника abc якщо a(-1; 2) b(3; 7) c(2; -1)

Даны вершины треугольника A(-1; 2), B(3; 7), C(2; -1).

Вектор AВ = ((3-(-1)); (7-2)) = (4; 5). Модуль равен √(16 + 25) = √41.

Вектор AС = ((2-(-1)); (-1-2)) = (3; -3). Модуль равен √(9 + 9) = √18 = 3√2.

cos A = (4*3 + 5*(-3))/(√41*3√2) = -3/(3√82)= -1/√82 ≈ -0,11043.    

Угол А = arccos(-0,11043) = 96,34019°.

Вектор ВA = -AB = (-4; -5). Модуль равен √(16 + 25) = √41.

Вектор BС = ((2-3); (-1-7)) = (-1; -8). Модуль равен √(1 + 64) = √65.

cos B = (-4*(-1) + (-5)*(-8))/( √41*√65) = 44/√2665 ≈ 0,852323.

Угол B = arccos(0,852323) = 31,53479°.

Вектор СВ = -BC = (1; 8). Модуль равен √(1 + 64) = √65.

Вектор СА = -AC = (-3; 3). Модуль равен √(9 + 9) = √18 = 3√2.

cos C = (1*(-3) + 8*3))/( √13*3√2) = 21/3√26 =7/√26  ≈ 0,613941.

Угол C = arccos(0,613941) = 52,12502°.