Знайдіть центральний кут і кількість сторін правильного
многокутника зі стороною 6 см, якщо радіус кола, вписаного в цей
многокутник, дорівнює 3√3 см

Ответ:

Центральный угол равен 60°.

Количство сторон - 6.

Объяснение:

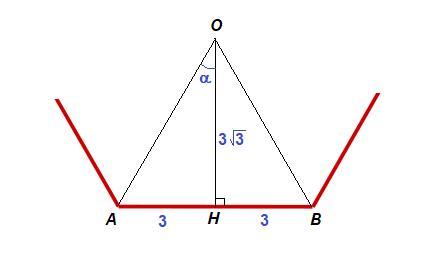
Соединим центр О правильного многоугольника с двумя соседними вершинами А и В.

Получим равнобедренный треугольник АОВ (АО = ВО как радиусы).

Проведем ОН⊥АВ. ОН - высота, медиана и биссектриса. Так же ОН - радиус вписанной в многоугольник окружности.

ОН = 3√3 см,  АВ = 6 см

АН = ВН = 3 см

Из прямоугольного треугольника АОН:

α = 30°

∠АОВ = 2α = 2 · 30° = 60° - центральный угол многоугольника.

Тогда количество его сторон:

n = 360° : 60° = 6