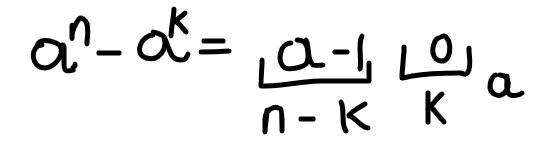Значение арифметического выражения 5^1200 +25^1000 - 5^100 записали в
системе счисления с основанием 5. Сколько цифр «4» содержится в этой
записи?
Ответы на вопрос
Ответ:Сначала приведу примеры степеней в нашей, десятичной системе:
То есть, если возводить основание системы в какую то целую степень, то число нулей равно показателю этой степени.
Так вот, в других системах так же. Например, если возводить 5 в какую то степень, то в пятеричной системе это число будет выглядеть как единица с числом нулей, равным показателю степени:
Приведём все слагаемые в этом выражении к виду степени с основанием 5:
Далее, представим как они выглядят в пятеричном виде (начнём с самого большого слагаемого):
(всего 216 нулей)
(всего 188 нулей)
(всего 3 нуля)
Если сложить в пятеричном виде первые два числа, то мы получим число, которое выглядит так:
100....00100000...00000 (пятеричное)
(сначала идёт единица, затем 216-188-1=27 нулей, далее единица, далее 188 нулей)
Если теперь из этого вычесть то получим вот что:
100....00044444...44000 (пятеричное)
(сначала идёт единица, затем 27+1=28 нулей, далее 188-3=185 четвёрок, далее 3 нуля)
Вот мы и получили ответ на вопрос в этой задаче- четвёрок тут ровно 185 штук.
Почему там появились четвёрки? Опять приведу примеры из десятичной системы:
А в пятеричной- то же самое, но будут четвёрки:
(ведь тут пять цифр- от 0 до 4, а после 4 идёт уже 10)
Теперь, пример посложнее в десятичной системе:
(то есть, произошло последовательное заимствование единицы из следующих разрядов, пока не дошло до разряда, в котором не было нуля)
А вот, то же самое, но в пятеричной системе:
Объяснение:
Сначала приводим все числа к одному основанию и выставляем их в порядке убывания. Обратите внимания, что при сложении цифре 4 взяться некуда. Единственное, откуда они могут появиться, это при вычитании, поэтому только это действие мы и разбираем. Формула, которой мы воспользовались представлена на втором скриншоте