Здравствуйте, сложные задачи по алгебре, помогите кто нибудь решить задачу пожалуйста , скиньте пример хотябы или посоветуйте как решить , пункт б
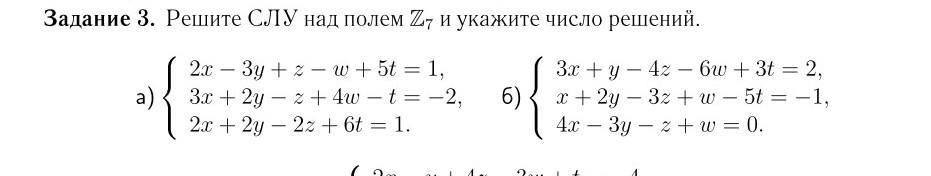
Ответы на вопрос
Ответ:
343 решений.
Объяснение:
Напомним, что это поле остатков при делении на 7; оно состоит из чисел 0, 1, 2, 3, 4, 5, 6. Если, скажем, складываются числа 4 и 5, то надо писать не 9, а 2, если перемножаешь 2 и 4, то надо писать не 8, а 1; поэтому элементом, обратным к 2, является 4. Напишем ради интереса обратные ко всем ненулевым элементам:
Напишем для коллекции и противоположные ко всем элементам:
Поэтому при желании мы можем в системе заменить, скажем, коэффициент минус шесть на 1, минус 5 на два. Такие вещи мы будем делать без объяснений. Будем решать систему обычным методом Гаусса. Из технических соображений я не рисую черту, отделяющую основную матрицу коэффициентов от столбца свободных членов. Имеем
Для упрощения 5-го столбца добавим ко второй строчке учетверенную первую:
Добавим ко второй строчке удвоенную третью, а из первой вычтем третью:
Базисные переменные w и t. Чтобы сделать козффициент при t равным 1, домножим первую строчку на 5. Нулевую строчку отбросим:
Получили систему
Свободные переменные x, y, z; пусть
Каждая из произвольных постоянных может принимать 7 значений, поэтому мы имеем решений.