Здравствуйте! Решите, пожалуйста, 2 уравнения, как у меня на примере, точь в точь и никаким другим способом! Кстати, у меня на примере решение 1-го из уравнений, правильно ли оно? Прошу решить! Заранее спасибо ВАМ
Приложения:
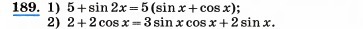

Igor171717:
Нет, нет, точь в точь имею ввиду по такому же принципу что и я решил, т.е по такому же ходу решения
Скажите, а где у меня ошибка?
что означает arcsin(√8) ?????
не знаю
аа
корнет нет!?
а так верно?
Жду решгения
Спасибо
задание Русский язык, поэтому грубо → sinx +cosx < 2
Ответы на вопрос
Ответил oganesbagoyan
4
task/25081778
-------------------
* * * sin²x +cos²x =1 ; sin2x =2sinx*cosx ; 5 =4+1 =4 + ( sin²x + cos²x ) * * *
----------------------
189 1) 5+sin2x =5(sinx+cosx) ⇔
4+sin²x +2sinx*cosx+cos²x =5(sinx+cosx)⇔
(sinx+cosx)² - 5(sinx+cosx)²+4 = 0 пусть sinx+cosx = t , тогда
t² -5t +4 =0 ⇒[ t=4 ,
[ t= 1.
[ sinx +cosx = 4 > √2 _не имеет решения
[ sinx +cosx =1.
√2cos(x -π/4) =1 ;
cos(x-π/4) =1/√2 ;
x-π/4 =± π/4+2πn , n∈ℤ
x= 2πn или x= π/2 +2πn , n∈ℤ.
ответ : 2πn ; π/2 +2πn , n∈ℤ.
------- P.S. -------
sinx +cosx =√2sin(x+π/4) ⇒ - √2 ≤ sinx +cosx ≤√2
sinx +cosx =√2cos(x-π/4)
----------------------
189 2) 2+2cosx =3sinxcosx +2sinx ⇔4+4cosx =6sinxcosx +4sinx ⇔
4- 6sinxcosx +4(cosx-sinx) =0 ;
1+3cos²x +3sin²x - 6sinxcosx +4(cosx-sinx)=0 ;
1+3(cos²x - 2sinxcosx +sin²x) +4(cosx-sinx)=0 ;
3(cosx - sinx)² +4(cosx-sinx) +1 =0 ; замена cosx-sinx= t
3t² +4t +1 =0 , D/4 =2²-3=1;
t ₁ =(-2-1)/3 = -1;
t₂ = (-2+1)/3= -1/3 .
----------
a) cosx - sinx =-1 ;
√2cos(x++π/4) = -1 ;
cos(x+π/4) = -1/√2 ;
x+π/4 = ± (π-π/4) +2πn , n∈ℤ ;
x+π/4 = ± 3π/4 +2πn ,n∈ℤ иначе
x = -π+2πn ; x =π/2+2πn , n∈ℤ .
---
б) cosx - sinx =-1/3 ;
√2cos(x+π/4) = -1/3 ;
cos(x+π/4) = -1/3√2
x+π/4 = ± (π-arccos1/3√2) +2πn , n∈ℤ ;
x= - π/4 ± (π-arccos1/3√2) +2πn , n∈ℤ ;
-------------------
* * * sin²x +cos²x =1 ; sin2x =2sinx*cosx ; 5 =4+1 =4 + ( sin²x + cos²x ) * * *
----------------------
189 1) 5+sin2x =5(sinx+cosx) ⇔
4+sin²x +2sinx*cosx+cos²x =5(sinx+cosx)⇔
(sinx+cosx)² - 5(sinx+cosx)²+4 = 0 пусть sinx+cosx = t , тогда
t² -5t +4 =0 ⇒[ t=4 ,
[ t= 1.
[ sinx +cosx = 4 > √2 _не имеет решения
[ sinx +cosx =1.
√2cos(x -π/4) =1 ;
cos(x-π/4) =1/√2 ;
x-π/4 =± π/4+2πn , n∈ℤ
x= 2πn или x= π/2 +2πn , n∈ℤ.
ответ : 2πn ; π/2 +2πn , n∈ℤ.
------- P.S. -------
sinx +cosx =√2sin(x+π/4) ⇒ - √2 ≤ sinx +cosx ≤√2
sinx +cosx =√2cos(x-π/4)
----------------------
189 2) 2+2cosx =3sinxcosx +2sinx ⇔4+4cosx =6sinxcosx +4sinx ⇔
4- 6sinxcosx +4(cosx-sinx) =0 ;
1+3cos²x +3sin²x - 6sinxcosx +4(cosx-sinx)=0 ;
1+3(cos²x - 2sinxcosx +sin²x) +4(cosx-sinx)=0 ;
3(cosx - sinx)² +4(cosx-sinx) +1 =0 ; замена cosx-sinx= t
3t² +4t +1 =0 , D/4 =2²-3=1;
t ₁ =(-2-1)/3 = -1;
t₂ = (-2+1)/3= -1/3 .
----------
a) cosx - sinx =-1 ;
√2cos(x++π/4) = -1 ;
cos(x+π/4) = -1/√2 ;
x+π/4 = ± (π-π/4) +2πn , n∈ℤ ;
x+π/4 = ± 3π/4 +2πn ,n∈ℤ иначе
x = -π+2πn ; x =π/2+2πn , n∈ℤ .
---
б) cosx - sinx =-1/3 ;
√2cos(x+π/4) = -1/3 ;
cos(x+π/4) = -1/3√2
x+π/4 = ± (π-arccos1/3√2) +2πn , n∈ℤ ;
x= - π/4 ± (π-arccos1/3√2) +2πn , n∈ℤ ;
Ответил Аноним
2
Первое уравнение, см. решение.
Приложения:

Новые вопросы