Здравствуйте помогите пожалуйста с задачей.
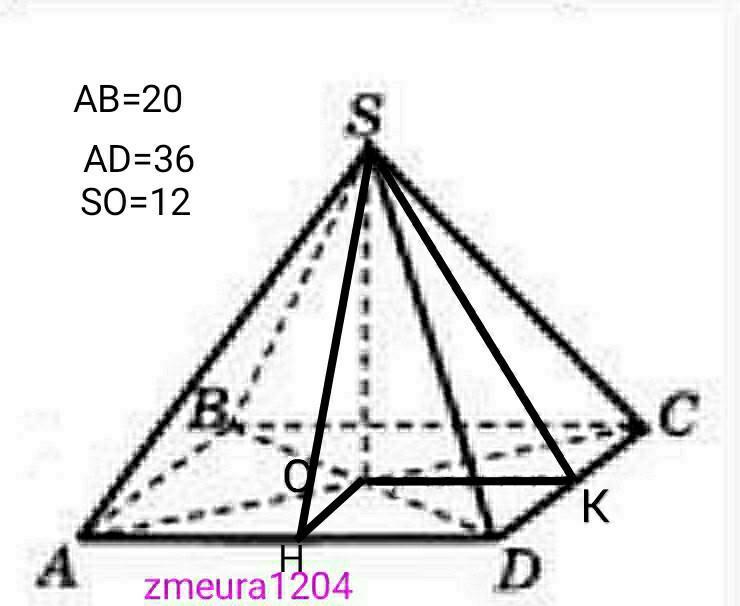
Знайти площу бічної та повної поверхні чотирикутної піраміди якщо основа прямокутник зі сторонами 20 см і 36 см а висота піраміди 12 см

Ответ:

Sбіч=120√13+72√61 см²

Sпов=720+120√13+72√61 см²

Объяснение:

OK=AD/2=36/2=18см

∆SOK- прямокутний трикутник

За теоремою Піфагора:

SK=√(SO²+OK²)=√(12²+18²)=√(144+324)=

=√468=6√13 см

S(∆SDC)=½*DC*SK=½*20*6√13=60√13 см²

∆SDC=∆SBA;

OH=AB/2=20/2=10см

∆SOH- прямокутний трикутник.

За теоремою Піфагора:

SH=√(SO²+OH²)=√(12²+10²)=√(144+100)=

=√244=2√61 см

S(∆SAD)=½*AD*SH=½*36*2√61=36√61см²

∆SAD=∆SBC

Sбіч=2*S(∆SDC)+2*S(∆SAD)=

=2*60√13+2*36√61=120√13+72√61 см²

Sосн=АВ*АD=20*36=720см²

Sпов=Sосн+Sбіч=720+120√13+72√61 см²