Алгебра, вопрос задал Astapenko1593 , 11 месяцев назад

Здравствуйте, помогите пожалуйста. Найти производные первого порядка данных функций,
используя правила вычисления производных.

Приложения:

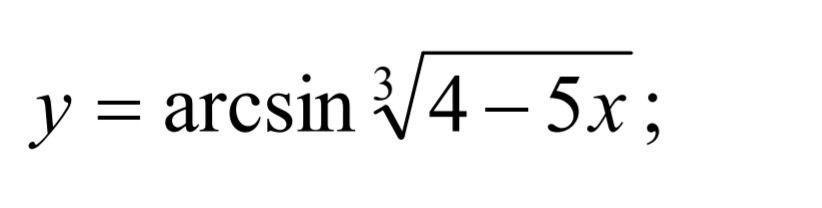
Ответы на вопрос

Ответил NNNLLL54

Ответ:

Найти производную 1-го порядка . Используем правила вычисления производных и таблицу производных .

Производная сложной функции равна : $\bf \Big(f\Big(u(x)\Big)\Big)'=f'_{u}\cdot u'_{x}$ .

$\bf y=arcsin\, \sqrt[3]{\bf 4-5x}\ \ ,\ \ \ \ u=\sqrt[3]{\bf 4-5x}\\\\y'=\dfrac{1}{\sqrt{1-\sqrt[3]{\bf (4-5x)^2}}}\cdot \Big(\sqrt[3]{\bf 4-5x}\Big)'=\dfrac{1}{\sqrt{1-\sqrt[3]{\bf (4-5x)^2}}}\cdot \Big((4-5x)^{^{\frac{1}{3}}}\Big)'=\\\\\\=\dfrac{1}{\sqrt{1-\sqrt[3]{\bf (4-5x)^2}}}\cdot \dfrac{1}{3}\cdot (4-5x)^{^{-\frac{2}{3}}}\cdot (-5)=\dfrac{1}{\sqrt{1-\sqrt[3]{\bf (4-5x)^2}}}\cdot \dfrac{-5}{3\, \sqrt[3]{\bf (4-5x)^2}}$