Здравствуйте, помогите пожалуйста
Ответы на вопрос
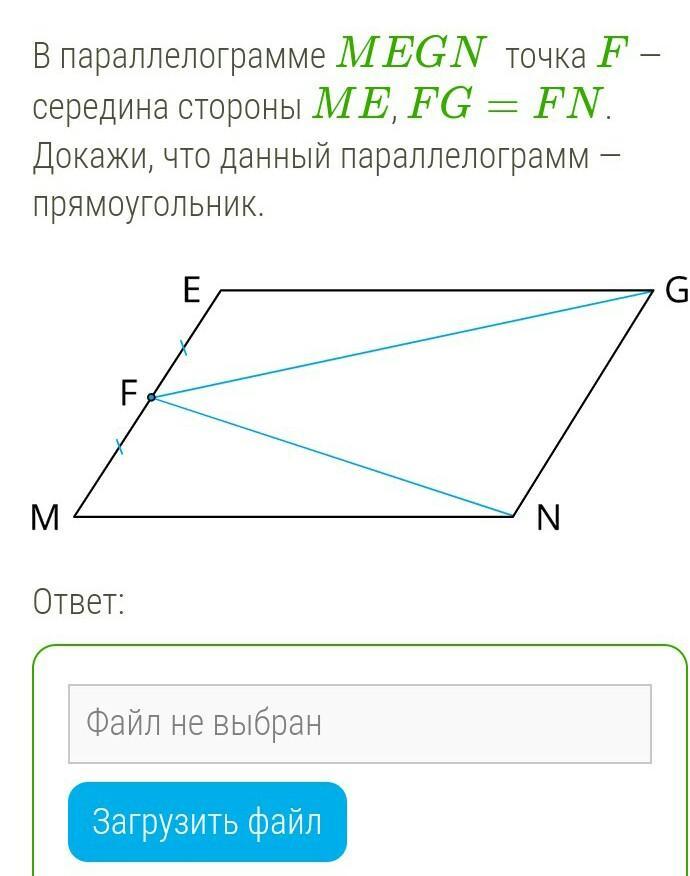
В параллелограмма MEGN точка F - середина стороны ME, FG = FN. Докажи, что данный параллелограмм - прямоугольник.
Доказательство:
У параллелограмма противоположные стороны равны, т.е. . По условию,
- середина стороны
, следовательно,
и
отсюда следует, что треугольники FEG и MFN равны по трем сторонам. У равных треугольников соответствующие элементы равны, т.е.
∠MEG = ∠FMN, а в четырехугольника сумма внутренних углов равна 360°, т.е. 4∠M = 360° ⇒ ∠M = 90°
∠E = ∠M = ∠N = ∠G = 90°
Все углы равны по 90° и противоположные стороны параллелограмма равны, значит MEGN - прямоугольник.
ΔМFN=ΔEFG по 3 признаку равенства треугольников.
1. EF=МF по условию
2. FG= FN по условию
3. EG=МN по свойству противолежащих сторон в параллелограмме.
Из равенства треугольников следует равенство углов FМN и FEG.
Но по свойству углов параллелограмма, прилежащих к одной стороне МЕ, эти углы в сумме составляют 180°, значит, каждый - по 90°, а параллелограмм даже с одним прямым углом - прямоугольник. Требуемое доказано.