Математика, вопрос задал homieea8 , 2 года назад

Записать комплексные числа в тригонометрической и показательной формах :

Приложения:

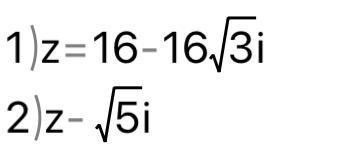
Ответы на вопрос

Ответил Магистр1Йода

$z=\sqrt{6} *e^{i\frac{\pi}{2} }$ Ответ:

Пошаговое объяснение:1)

$r=\sqrt{16^2+(-16)^2} =\sqrt{512} \\artg\alpha(\frac{-16}{16})=tg(-1)=\frac{7\pi }{4}$

$r(cos\alpha +isin\alpha )=\sqrt{512} (cos\frac{7\pi }{4} +sin\frac{7\pi }{4} )=\sqrt{512} (\frac{\sqrt{2} }{2}-i\frac{\sqrt{2} }{2} )$ -тригонометрическая форма

$r*e^{i\alpha } =\sqrt{512}*e^{i*\frac{7\pi }{4} }$ -показательная форма

$r=\sqrt{0^2+(\sqrt{5})^2 } =\sqrt{5} \\tg\alpha =(\frac{-\sqrt{5} }{0} )=>artg(\frac{-\sqrt{5} }{0} )=\alpha=\frac{\pi}{2} ;z=\sqrt{5} (cos(\frac{\pi}{2} )+isin(\frac{\pi }{2} )=\sqrt{5} (0+i)=\sqrt{5}i$ -тригонометрическая

$z=\sqrt{5} *e^{i\frac{\pi}{2} }$ -показательная

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Окружающий мир, 1 год назад

Сообщение флаге россии.Коротенькое...

Русский язык, 1 год назад

какой размер оперения синицы (в сантиметрах)...

Українська мова, 2 года назад

94 I. Спишіть речення, розставляючи пропущені розділові знаки. 1. Баба Марина довгий свій вік трави сушила у хаті м'яту любистоклиповий цвіт. (С. Решетова). 2. Ми полюбили все і гомін вулиці і тишу...

Математика, 2 года назад

100 баллов!!!!! Математика 8 класс!!!! Выполните задание. Впишите в поля для ответа только числа. Замените в выражении значки, так чтобы получилось тождество.

Алгебра, 7 лет назад

Найдите область определения функции...

Литература, 7 лет назад

Опишите Андрия и Остапа, из повести Тарас Бульба...