Алгебра, вопрос задал aloloy , 9 лет назад

Задания с логарифмами

Приложения:

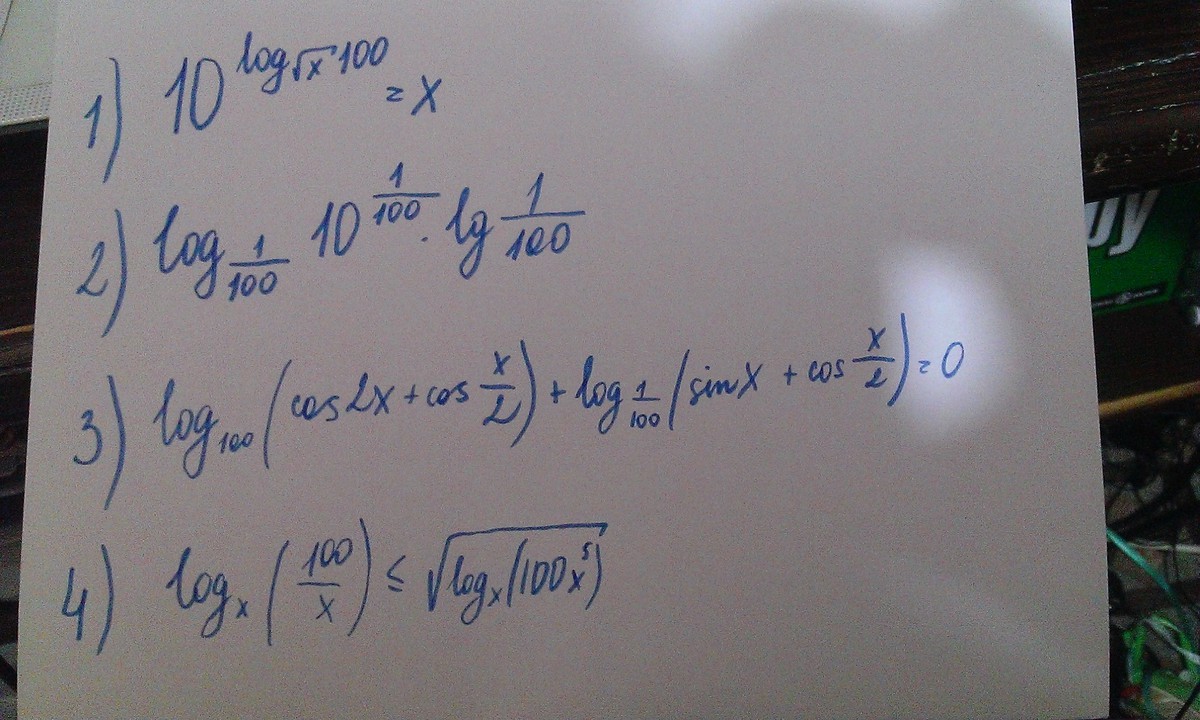
Ответы на вопрос

Ответил Artem112

$10^{log_ {sqrt{x}}100 }=x$
ОДЗ:
$left { {{x>0} atop {x neq 1} right.$
$10^{log_ {sqrt{x}}100 }=x \ log_ {sqrt{x}}10^2 =lg x \ 2log_ {sqrt{x}}10 =lg x \ 4log_ {x}10 =lg x \ frac{4}{lg x} =lg x \ lg ^2x=4 \ lg x=pm2 \ x_1=10^2=100 \ x_2=10^{-2}=0,01$
Ответ: 100 и 0,01

$log_ frac{1}{100} 10^{ frac{1}{100} }lg frac{1}{100} = log_ {10^{-2}}10^{10^{-2}}lg10^{-2} = \ =10^{-2}log_ {10^{-2}}10log_{10}10^{-2} =10^{-2}=0,01$

$log_{100}(cos2x+cos frac{x}{2} )+log_{ frac{1}{100} }(sin x+cos frac{x}{2} )=0 \ log_{100} (cos2x+cos frac{x}{2} )-log_{100}(sin x+cos frac{x}{2} )=0 \ log_{100} frac{cos2x+cos frac{x}{2}}{sin x+cos frac{x}{2}}=0 \ frac{cos2x+cos frac{x}{2}}{sin x+cos frac{x}{2}}=1 \ cos2x+cos frac{x}{2}=sin x+cos frac{x}{2}} \ cos2x=sin x \ 1-2sin^2x=sin x \ 2sin^2 x+sin x-1=0 \ D=1+8=9$
$sin x= frac{-1-3}{4} =-1 \ x=frac{3 pi }{2}+2 pi n, nin Z \ sin x=frac{-1+3}{4} = frac{1}{2} \ x= frac{ pi }{6} +2 pi k, kin Z \ x= frac{5 pi }{6} +2 pi l, lin Z$
Однако при подстановке корней из первой серии первый логарифм не имеет смысла:
$cos (2cdot frac{3 pi }{2} )+cos frac{3 pi }{4} =-1- frac{2}{2} <0$
При подстановке корней из второй серии при нечетных k не имеет смысла второй логарифм:
$sin frac{13 pi }{6} +cos frac{13 pi }{12}=sin frac{ pi }{6} -cos frac{ pi }{12}=frac{1 }{2} -cos frac{ pi }{12}<0$
Ответ: $frac{ pi }{6} +4 pi m$ и $frac{5 pi }{6} +2 pi l$ , где m и l - целые числа.

$log_x( frac{100}{x} )< sqrt{log_x(100x^5)}$
ОДЗ:
$log_x(100x^5) geq 0 \ log_x10^2+log_xx^5 geq 0 \ 2log_x10+5 geq 0 \ frac{2}{lg x} +5 geq 0 \ frac{2+5lg x}{lg x} geq 0 \ lg x leq -frac{2}{5} : x leq 10^{-0,4} \ lg x >0: x>1 \ xin(0;10^{-0.4}]cup(1;+infty)$
Решаем:
$log_x( frac{100}{x} )< sqrt{log_x(100x^5)} \ log_x100-log_xx< sqrt{log_x100+log_xx^5} \ log_x100-1< sqrt{log_x100+5} \ (log_x100-1)^2<log_x100+5 \ log_x^2100-2log_x100+1<log_x100+5 \ log_x^2100-3log_x100-4<0 \ <log_x100=log_x10^2=2log_x10= frac{2}{lg10} > \ ( frac{2}{lg10})^2-3cdot frac{2}{lg10}-4<0 \ D=3^2+4cdot4=25 \ frac{2}{lg10}= frac{3+5}{2} =4 \ frac{2}{lg10}= frac{3-5}{2} =-1$
1)
$frac{2}{lg10} geq -1 \ frac{2+lg x}{lg x} geq 0 \ lg x=-2: x=10^{-2}=0,01 \ lg x=0: x=10^0=1 \ xin(-infty;0,01]cup[1;+infty)$
2)
$frac{2}{lg10} leq 4 \ frac{2-4lg x}{lg x} geq 0 \ lg x= frac{1}{2} : x= sqrt{10} \ lg x=0: x=10^0=1 \ xin(-infty; 1]cup[ sqrt{10} ;+infty)$
Объединяем 1) и 2):
$xin(-infty;0.01]cup(1)cup[ sqrt{10} ;+infty)$
Так как при решении мы возвели в квадрат обе части, то возможно мы потеряли серию решений - если левая часть отрицательно, то при допуститом ОДЗ неравенство выполняется. Найдем все значения х, при которых левая часть отрицаьтельная и добавим их к полученным ренее решениям.
$log_x frac{100}{x} <0 \ log_x100-log_xx <0 \ log_x10^2-1<0 \ 2log_x10-1<0 \ frac{2-lg x}{lg x} <0 \ frac{lg x-2}{lg x} >0 \ lg x=0: x=10^0=1 \ lg x=2: x=10^2=100 \ xin(-infty; 1)cup(100;+infty)$
Объединяя полученные ранее решения и учитывая ОДЗ, получим:
$xin (0;10^{-0.4})cup[ sqrt{10} ;+infty)$
Ответ: $xin (0;10^{-0.4})cup[ sqrt{10} ;+infty)$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Литература, 2 года назад

Примеры к пословице “Что мне до него - было б мне хорошо" срочно!

Математика, 2 года назад

Арбуз разрезали на 7 равных кусков и 2 дали Ире. Какая часть арбуза у Иры? Как это можно записать?

Математика, 9 лет назад

Помогите пожалуйста№496...

История, 9 лет назад

Можно ли утверждать,что власть князя Ярослава Мудрого на руси была такой же как власть короля франков Карла Великого?

История, 9 лет назад

какие формы правления существовали в городах-государствахантичной европы??-помогите плиз...

Биология, 9 лет назад

в ротовую полость открываются протоки слюнных желез? три правильных ответа из шести предложенных должно быть:) 1.желательных 2. околоушных 3. пищеварительных 4. подъязычных 5. подчелюстных...