Задание во вложении)
Надеюсь на подробное объяснения.
Приложения:
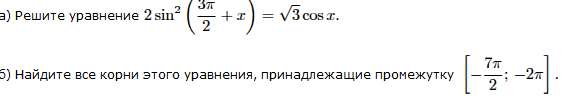
Ответы на вопрос
Ответил bearcab
0
Воспользуемся формулой синуса суммы
Тогда вычислим просто
Преобразуем уравнение к виду
Получается два решения
Это - первая серия решений.
Это - вторая серия решений.
Пусть в первой серии решений n=(-4), тогда
Пусть в первой серии решений n=(-3), тогда
При других n решения "вылетают" из заданного промежутка.
Несколько сложнее со второй серией решений.
При к=(-1) снова получаем только одно решение
При остальных к - решения "вылетают" из отрезка
Получается только 3 решения
</p>
<p> </p>
<p><img src=[/tex]x_{12}=-frac{5pi}{2}" title="x_{11}=-frac{7pi}{2}" title="x_{12}=-frac{5pi}{2}" title="x_{11}=-frac{7pi}{2}" alt="x_{12}=-frac{5pi}{2}" title="x_{11}=-frac{7pi}{2}" />
Новые вопросы