Математика, вопрос задал Lena3216548 , 1 год назад

Задание просто не даётся, помогите пожалуйста

Приложения:

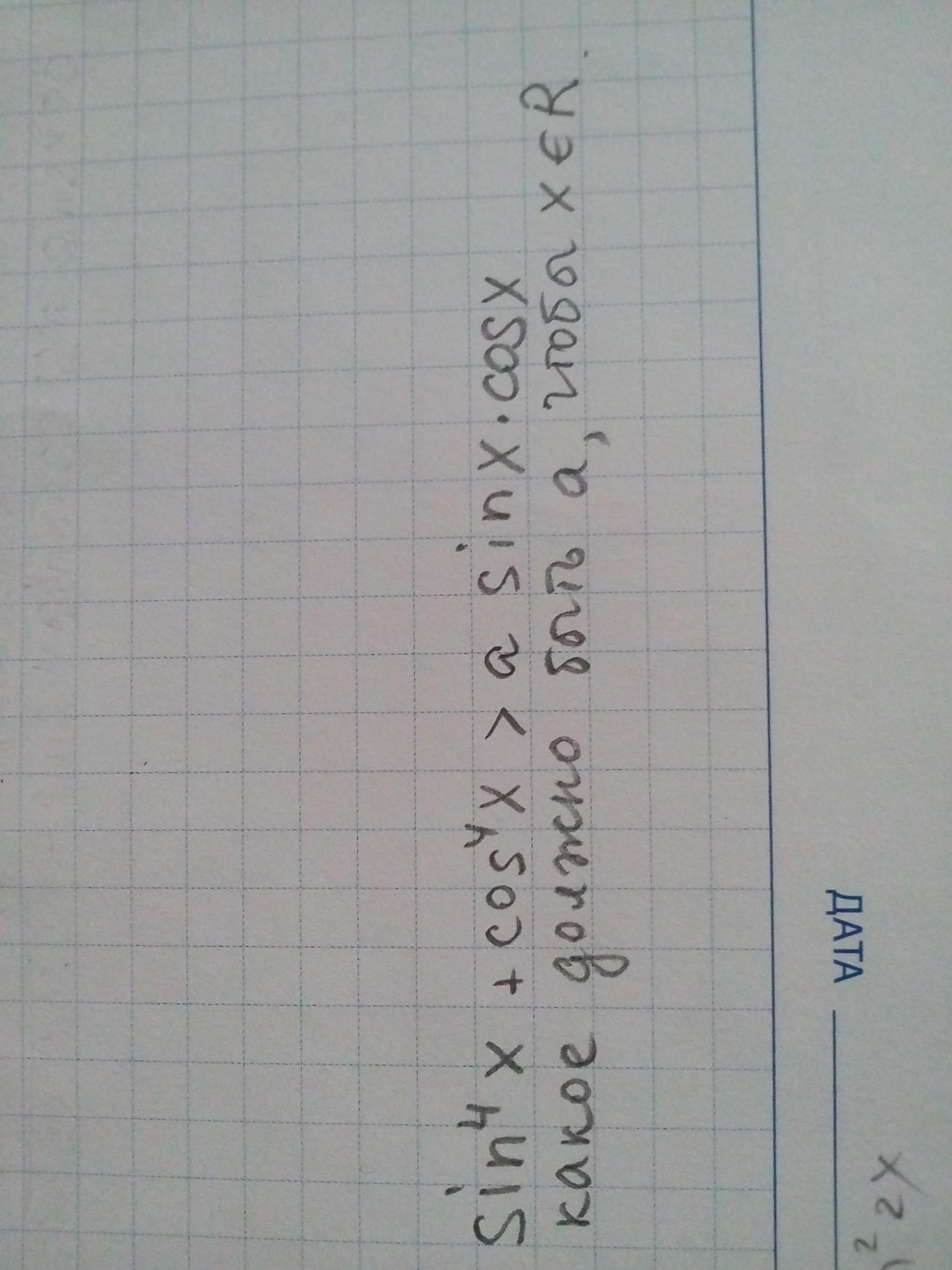
Ответы на вопрос

Ответил Аноним

$\sin^4x+\cos^4x>a\sin x\cos x\\\left(\cos^2x\right)^2+2\sin^2x\cos^2x+\left(\sin^2x\right)^2-2\sin^2x\cos^2x>\frac a2\sin2x\\\left(\cos^2x+\sin^2x\right)^2-\frac12\sin^2x\cos^2x>\frac a2\sin2x\\1-\sin^22x>\frac a2\sin2x\\\sin^22x+a\sin2x<2\\\sin2x\cdot(\sin2x+a)<2$

sin2x принимает значения от -1 до 1. Рассмотрим значения последнего выражения в этих точках:

$\sin2x=-1:\\-1\cdot(-1+a)<2\\1-a<2\\a>-1\\\\\sin2x=1:\\1\cdot(1+a)<2\\1+a<2\\a<1$

Если взять любые значения sin2x из интервала (-1; 1), то параметр a будет будет либо больше 1, либо меньше -1.

Таким образом, для того, чтобы неравенство выполнялось для любых x, a должно принадлежать интервалу (-1; 1).

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

1 Найдите пересечение и объединение промежутков 1 -4 2...

Математика, 1 год назад

2. Мiж якими двома сусідніми цілими числами міститься число - 0,5: a) 0 i l; б) -2i-1; B)-li0; г) -5 1 0. срочноооо...

Математика, 1 год назад

З одного міста в інше виїхала машина першу третину шляху вона їхала зі швидкістю 50 км год а другу третину 60 км год а останній 75 км год чому дорівнює середня швидкість машини на всьому маршруті?

Русский язык, 1 год назад

Прочитай текст. Озаглавь каждую часть. Запиши текст по плану.

Другие предметы, 6 лет назад

teps GOSENN древними людьми х Расположи этапы развития первобытного искусства в правильном порядке. 1 Появление петроглифов 1 Создание «Палеолитических Бенер» был. Расцвет пещерной росписи...

Алгебра, 6 лет назад

5 3/1•(2 5/8) помогите ...