Математика, вопрос задал Reideen , 2 года назад

Задание приложено...

Приложения:

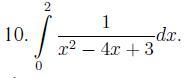
Ответы на вопрос

Ответил malika240318

Ответ:

Ответ будет: -1/2*ln3, (ln1=0)

Приложения:

malika240318: отметьте как лучший ответ, спасибо!

Ответил mathkot

Ответ:

Интеграл расходится

Пошаговое объяснение:

$\displaystyle \int\limits^{2}_{0} {\frac{1}{x^{2} - 4x + 3} } \, dx$ - интеграл расходится

Найдем область определения подынтегральной функции для чего решим следующие уравнение:

$x^{2} - 4x + 3 = 0$

$D = (-4)^{2} - 4 \cdot 1 \cdot 3 = 16 - 12 = 4 = 2^{2}$

$x_{1} = \dfrac{4 + 2}{2} = \dfrac{6}{2} = 3$

$x_{2} = \dfrac{4 - 2}{2} = \dfrac{2}{2} = 1$

Таким образом подынтегральная функция определена на множестве $\mathbb R$ , кроме точек 1 и 3.

Так как интегрирование происходит в пределах от 0 до 2, а знаменатель дроби не может равняться нулю, то в точке 1 функция терпит разрыв, таким образом интеграл $\displaystyle \int\limits^{2}_{0} {\frac{1}{x^{2} - 4x + 3} } \, dx$ - несобственный интеграл 2 рода.

Таким образом, так как точка 1 принадлежит промежутку интегрирования [0;2] и лежит внутри данного промежутка, то:

$\displaystyle \int\limits^{2}_{0} {\frac{1}{x^{2} - 4x + 3} } \, dx = \int\limits^{1}_{0} {\frac{1}{x^{2} - 4x + 3} } \, dx + \int\limits^{2}_{1} {\frac{1}{x^{2} - 4x + 3} } \, dx$

Рассмотрим неопределенный интеграл $\displaystyle \int {\frac{1}{x^{2} - 4x + 3} } \, dx$ .

$\displaystyle \int {\frac{1}{x^{2} - 4x + 3} } \, dx = \int {\frac{1}{x^{2} - 4x + 4 - 1} } \, dx =\int {\frac{1}{(x - 2)^{2} - 1} } \, d(x - 2) =$

$\displaystyle = \frac{1}{2} \ln \bigg| \frac{x - 2 - 1}{x - 2 + 1} \bigg| + C = \frac{1}{2} \ln \bigg| \frac{x - 3}{x - 1} \bigg| + C$

Рассмотрим несобственный интеграл 2 рода $\displaystyle \int\limits^{1}_{0} {\frac{1}{x^{2} - 4x + 3} } \, dx$ .

Воспользуемся обобщением формулы Ньютона-Лейбница для несобственных интегралов 2 рода:

$\displaystyle \int\limits^{1}_{0} {\frac{1}{x^{2} - 4x + 3} } \, dx = \frac{1}{2} \ln \bigg| \frac{x - 3}{x - 1} \bigg| \Bigg |^{1 - 0}_{0} = \lim_{x \to 1 - 0} \frac{1}{2} \ln \bigg| \frac{x - 3}{x - 1} \bigg| - \frac{1}{2} \ln \bigg| \frac{0 - 3}{0 - 1} \bigg|=$

$= -\infty - \dfrac{1}{2} \ln|3| = -\infty$

Так как интеграл $\displaystyle \int\limits^{1}_{0} {\frac{1}{x^{2} - 4x + 3} } \, dx$ - расходится, то расходится и интеграл $\displaystyle \int\limits^{2}_{0} {\frac{1}{x^{2} - 4x + 3} } \, dx$ .

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

напечатай,какой звуки(или звуки) обозначают выделенные буквы.С нас вода ручьЯми льётсЯ,а она ещЁ смеётсЯ:Вы действительно друзьЯ!Вас водой разлить нельзЯ!

Українська мова, 1 год назад

Скласти 5 речень з Узагальнувальним словом і однорідними членами речення...

Математика, 2 года назад

205. Розв'яжіть рiвняння: 1) (x+y)² +(x-1)² = 0; 2) (x− 2y + 1)² + x² − 6xy+9y² = 0; 3) |x+3y−5+ (7x−6y+4)² = 0; 4) x² + y² - 4x + бу+13=0; 5) x² + y² +8x−18y+97=0.

Физика, 2 года назад

допоможіть швидко будь ласка рішити задачі ...

История, 7 лет назад

Спартак и его роль в истории Рима...

Математика, 7 лет назад

Поезд отправился из Сочи в 11 часов 20 минут (время московское) и прибыл в Москву в 23 часа 20 минут следующих суток. Сколько часов поезд находился в пути?