Задание приложено...
Приложения:

Ответы на вопрос
Ответил mathkot
1
Ответ:
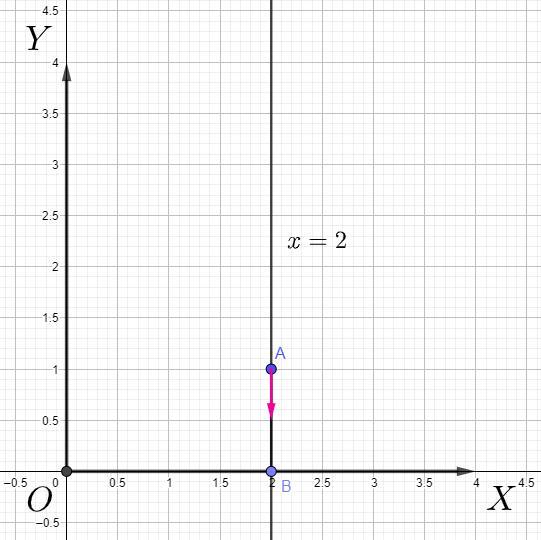
а)
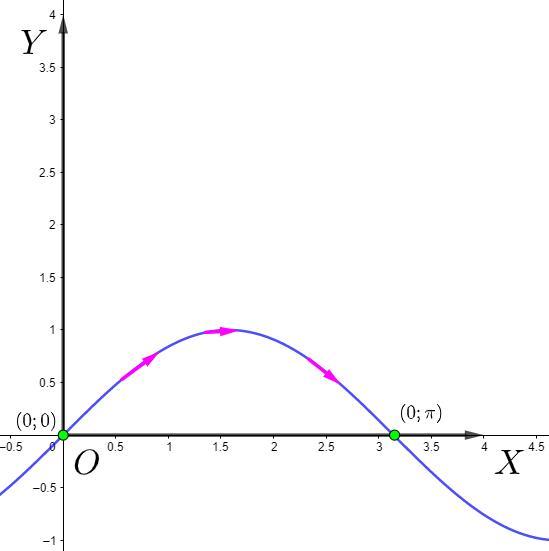
б)
Примечание:
Криволинейный интеграл второго рода по кривой имеет вид в общем виде:
- криволинейный интеграл 2 рода
Если кривая L задана уравнением y = y(x) , x ∈ [a;b], где
y = y(x) и ее производная y'(x) непрерывна на отрезке [a;b], то:
Объяснение:
а)
Где - отрезок
Так как , то уравнение прямой есть прямая
, то есть кривая
задается прямой:
б)
Где - дуга синусоиды
от
до
-------------------------------------------------------------
Интегрирование по частям:
----------------------------------------------------------------
Приложения:
kimmina7373:
здравствуйте вы не могли бы мне помочь с алгеброй пожалуйста умоляю
Новые вопросы