Математика, вопрос задал xolodok33331 , 6 лет назад

Задание по математическому анализу прикреплено ниже

Приложения:

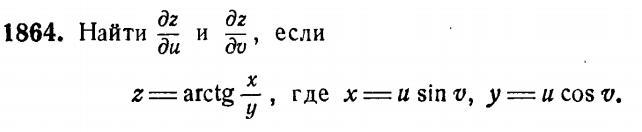
Ответы на вопрос

Ответил Miroslava227

Ответ:

Формулы:

$\frac{dz}{du} = \frac{dz}{dx} \times \frac{dx}{du} + \frac{dz}{dy} \times \frac{dy}{du} \\ \\ \frac{dz}{dv} = \frac{dz}{dz} \times \frac{dx}{dv} + \frac{dz}{dy} \times \frac{dy}{dv}$

(везде закругленная d)

$\frac{dx}{dx} = \frac{1}{1 + \frac{ {x}^{2} }{ {y}^{2} } } \times \frac{1}{y} = \frac{ {y}^{2} }{ {x}^{2} + {y}^{2} } \times \frac{1}{y} = \\ = \frac{y}{ {x}^{2} + {y}^{2} } \\ \frac{dz}{dy} = \frac{ {y}^{2} }{ {x}^{2} + {y}^{2} } \times ( - \frac{x}{ {y}^{2} } ) = - \frac{x}{ {x}^{2} + {y}^{2} }$

$\frac{dx}{du} = \sin(v) \\ \frac{dy}{du} = \cos(v) \\ \\ \frac{dx}{dv} = u \cos(v) \\ \frac{dy}{dv} = - u \sin(v)$

Собираем:

первая:

$\frac{dz}{du} = \frac{y}{ {x}^{2} + {y}^{2} } \times \sin(v) - \frac{x}{ {y}^{2} + {y}^{2} } \times \cos(v) = \\ = \frac{y \sin(v) - x \cos(v) }{ {x}^{2} + {y}^{2} }$

вторая:

$\frac{dz}{dv} = \frac{y}{ {x}^{2} + {y}^{2} } \times u \cos(v) + ( - \frac{x}{ {x}^{2} + {y}^{2} } ) \times ( - u \sin(v) ) = \\ = \frac{yu \cos(v) + xu \sin(v) }{ {x}^{2} + {y}^{2} }$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

География, 1 год назад

какие жизненно необходимые потребности человек удовлетворяет благодаря природе...

Математика, 1 год назад

Боковая сторона равнобедренного треугольника равна 75 мм,а периметр равен 20 см Найдите его основания...

Алгебра, 6 лет назад

Знайдіть загальний розвязок рівняння відносно а) y б) x 1) 5x-10y+=0 2) 2x-3y-1=0...

Обществознание, 6 лет назад

ДАЮ 50 БАЛЛОВ ПЖ ПОМОГИТЕ Предложите свое решение ситуации (не менее 5-ти предложений) У Вас есть друг, он постоянно ездит без билета в общественном транспорте. Если его встречает контролер, то...

Математика, 8 лет назад

Помогите пожалуйста 1/2-1/8 заранее спасибо...

Литература, 8 лет назад

сочинения на тему случай моей жизни ТОЛЬКО НЕ С ИНТЕРНЕТА ПОЖАЛУЙСТА...