задание найдите площадь фигуры ограниченной линиями у=х^3 y=0 x= -3 x=1 площадь нужно найти через интеграл там получаются две фигуры похожие на треугольник я не понимаю как расставить пределы интегрирования вот к примеру 1 и 0 я понимаю единица вверху 0 внизу единица больше нуля а вот расставляю -3 и 0 нуль вверху -3 внизу 0 больше -3 и получается отрицательное число а площадь отрицательной быть не может -81/4
Ответы на вопрос
Ответил ShirokovP
0
Здесь разбивается на 2 интеграла
И сумма будет положительный
Нижний интеграл брать с минусом не надо, его просто складывают с верхним
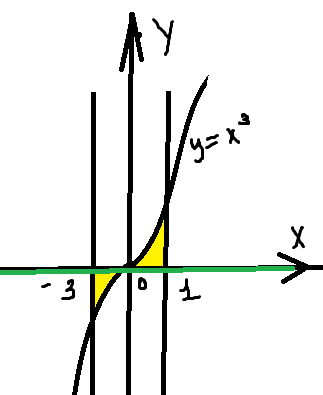
См. рисунок
И сумма будет положительный
Нижний интеграл брать с минусом не надо, его просто складывают с верхним
См. рисунок
Приложения:
Ответил ShirokovP
0
Обнови!!
Ответил oganesbagoyan
0
S =S₁+S₂= интеграл (0 - x³)dx + интеграл (x³ -0)dx =
a₁ = - 3 , b₁ =0 a₂ = 0 , b2 =1
-(x^4)/4 | a₁ = - 3 , b₁ =0 +(x^4)/4 | a₂ = 0 , b2 =1 = -((0^4)/4 -((-3)^4)/4) +(1^4)/4 -(0^4)/4 =
=81/4 +1/4 =82/4 =20,5.
* * * интеграл f(x)dx =F(x) | a -->b =F(b) - F(a) * * *
a -->b
a₁ = - 3 , b₁ =0 a₂ = 0 , b2 =1
-(x^4)/4 | a₁ = - 3 , b₁ =0 +(x^4)/4 | a₂ = 0 , b2 =1 = -((0^4)/4 -((-3)^4)/4) +(1^4)/4 -(0^4)/4 =
=81/4 +1/4 =82/4 =20,5.
* * * интеграл f(x)dx =F(x) | a -->b =F(b) - F(a) * * *
a -->b
Приложения:

Новые вопросы