Алгебра, вопрос задал AdrianDatiny , 6 лет назад

Задание 3 (16 баллов).

Решите систему уравнений:

Приложения:

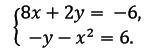
Ответы на вопрос

Ответил MatemaT123
2

Ответ:

(1; -7); \quad (3; -15);

Объяснение:

\displaystyle \left \{ {{8x+2y=-6} \atop {-y-x^{2}=6}} \right. \Leftrightarrow \left \{ {{8x+2y=-6} \atop {-2y-2x^{2}=12}} \right. \bigg |+

8x+2y-2y-2x^{2}=-6+12;

8x-2x^{2}=6 \quad | :(-2)

x^{2}-4x=-3;

x^{2}-4x+3=0;

Решим уравнение при помощи теоремы Виета:

\displaystyle \left \{ {{x_{1}+x_{2}=-(-4)} \atop {x_{1} \cdot x_{2}=3}} \right. \Leftrightarrow \left \{ {{x_{1}+x_{2}=4} \atop {x_{1} \cdot x_{2}=3}} \right. \Leftrightarrow \left \{ {{x_{1}=1} \atop {x_{2}=3}} \right. ;

x_{1}=1 \Rightarrow -y-1^{2}=6 \Rightarrow -y=6+1=7 \Rightarrow y=-7; \quad (1; -7);

x_{2}=3 \Rightarrow -y-3^{2}=6 \Rightarrow -y=6+9=15 \Rightarrow y=-15; \quad (3; -15);

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык, 1 год назад
Обозначь прилагательные-антонимы жестокий-милосерддный...
Русский язык, 1 год назад
Помогите пожалуйста! Задание 465...
Химия, 6 лет назад
Обчислити масу розчиненої речовини й розчинника що міститься в 400г 12%-го алюміній сульфату (АІ2(SO4)3)​...
Английский язык, 6 лет назад
Помогите пожалуйста ❤️ Прочитай приведённый ниже текст. Преобразуй слова, напечатанные заглавными буквами, так, чтобы они грамматически и лексически соответствовали содержанию текста. Заполни...
Химия, 8 лет назад
составьте уравнения нейтрализации между такими вещкствами: а)натрий гидроксид и ортофосфатная кислота б)кальций гидроксид и хлоридная кислота в)ферум (2) гидроксид и сульфатная кислота...
Математика, 8 лет назад
петя и митя идут в школу с одной и той же скоростью одной и той же дорогой . петя отстает от мити на 18 минут . сколько минут осталось идти пете , если мите осталось идти 5 минут .