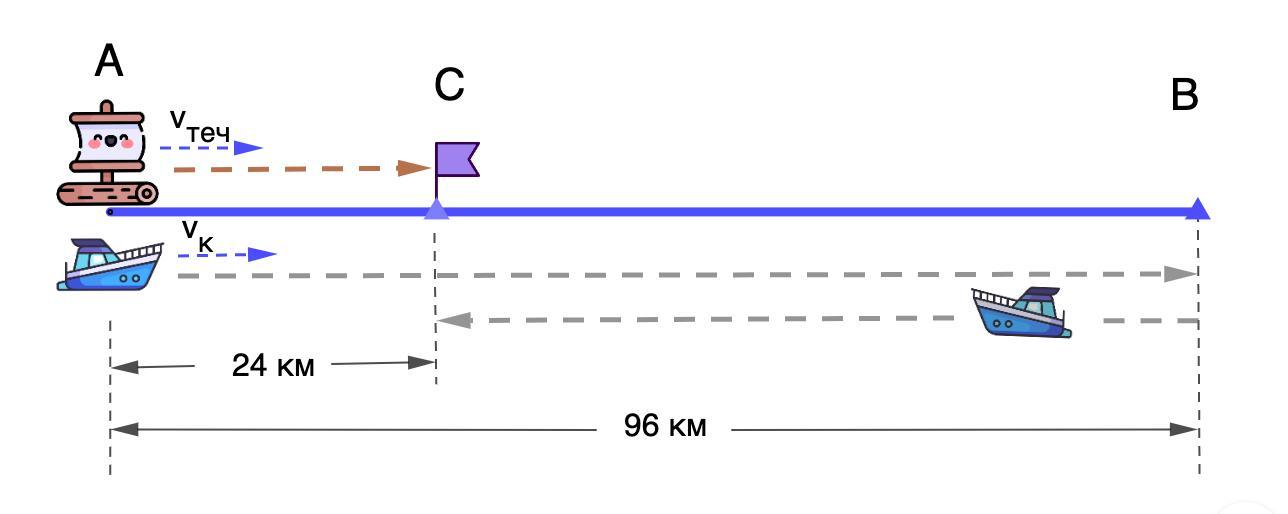
Математика, вопрос задал milenakarapetyan0507 , 6 лет назад

Задание 19: От пристани А одновременно
отправились вниз по течению катер и плот. Катер
спустился вниз по течению на 96 км, затем повернул
обратно и вернулся в А через 14 часов. Найти
скорость катера в стоячей воде и скорость течения,
если известно, что катер встретил плот на обратном
пути на расстоянии 24 км от А.

Ответы на вопрос

Ответил natalyabryukhova

Ответ:

Скорость катера в стоячей воде 14 км/ч; скорость течения 2 км/ч.

Пошаговое объяснение:

Требуется найти скорость катера в стоячей воде и скорость течения.

Вспомним формулы:

$\displaystyle \boxed {S=vt;\;\;\;\;\;v=\frac{S}{t};\;\;\;\;\;t=\frac{S}{v} }$

От пристани А одновременно отправились вниз по течению катер и плот.

Плот плывет за счет течения реки, значит скорость плота равна скорости течения реки.

Катер спустился вниз по течению на 96 км, затем повернул обратно и вернулся в А через 14 часов.

То есть, катер прошел по течению 96 км и против течения 96 км и затратил на весь путь 14 часов.

Vпо теч. = Vк. + Vтеч.;

Vпр. теч. = Vк. - Vтеч.

Пусть скорость катера - х км/ч; скорость течения - у км/ч.

Время катера по течению равно:

$\displaystyle \frac{96}{x+y}$ (ч)

Время катера против течения равно:

$\displaystyle \frac{96}{x-y}$ (ч)

Составим уравнение:

$\displaystyle \frac{96}{x+y}+ \frac{96}{x-y}=14$

Известно, что катер встретил плот на обратном пути на расстоянии 24 км от А.

Значит катер до встречи проплыл по течению 96 км и против течения

96 - 24 = 72 (км)

Плот до встречи проплыл 24 км.

При этом они затратили от момента отправления из пункта А одинаковое время:

Время плота:

$\displaystyle \frac{24}{y}$ (ч)

Время катера:

$\displaystyle \frac{96}{x+y} +\frac{72}{x-y}$

Составим уравнение:

$\displaystyle \frac{96}{x+y}+\frac{72}{x-y} =\frac{24}{y}$

Решим систему полученных уравнений:

$\displaystyle \left \{ {{\frac{96}{x+y}+ \frac{96}{x-y}=14} \atop { \frac{96}{x+y}+\frac{72}{x-y} =\frac{24}{y}}} \right. \\ \\$

Упростим первое уравнение:

$\displaystyle \frac{96}{x+y} +\frac{96}{x-y} =14\\\\\frac{96x-96y+96x+96y}{x^2-y^2} =14\\\\192x=14x^2-14y^2\;\;\;|:2\\\\96x-7x^2-7y^2=0$

Упростим второе уравнение и выразим х:

$\displaystyle \frac{96}{x+y}+\frac{72}{x-y}=\frac{24}{y} \\ \\\frac{96x-96y+72x+72y}{x^2-y^2} =\frac{24}{y} \\\\\frac{168x-24y}{x^2-y^2} =\frac{24}{y}\\ \\168xy-24y^2=24x^2-24y^2\\\\168xy-24x^2=0\\\\x(168y-24x) = 0\\\\x_1=0;\;\;\;\;\;x_2 = 7y$

x₁ не подходит по условию.

Подставим х = 7у в первое уравнение и найдем у.

$\displaystyle 96\cdot{7y}-7\cdot{49y^2+7y^2}=0\;\;\;|:7\\\\96y-48y^2=0\\\\y(96-48y)=0\\\\y_1=0;\;\;\;\;\;y=2$

y₁ не подходит.

⇒ у = 2; х = 7у = 14.

Скорость катера в стоячей воде 14 км/ч; скорость течения 2 км/ч.

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Запиши слова: стару...ки, о поез...ке,о п...годе, за с...бакой, ...пять в две группы. Каждую группу дополни примерами слов с такой же орфограммой. Четвероклассник, выполняя это задание дописал такие...

Русский язык, 1 год назад

1.Напишите,как называют жителей перечисленных городов и местностей.Суффиксы выделите. Тула,Кострома,Калуга,Курск,Смоленкс,Псков,Нижний Новгород,Север,Дальний Восток,.Урал. 2Запишите,как будут...

Русский язык, 6 лет назад

в чем различие имя существительно и глагол...

Русский язык, 6 лет назад

2. Подготовьте краткий пересказ рассказа К.Г. Паустовского «Старый повар» от 3-го лица.

Математика, 8 лет назад

Переведите в минуты и часы ; 280минут в часы и 4ч 50 минут в минуты...

Алгебра, 8 лет назад

Помогите решить 6* на корень из 48...