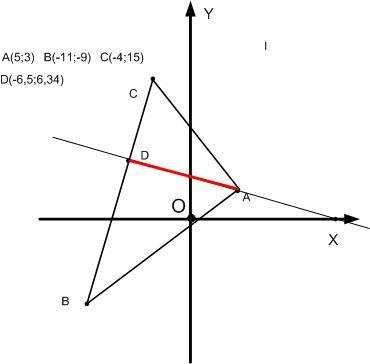
Задание № 1. Даны вершины А(5; 3), В(-11; -9), С(-4; 15) треугольника АВС. Требуется найти:
а) уравнение стороны АС;
б) длину высоты, проведенной из вершины А;
в) величину угла В (в радианах).
Ответы на вопрос
Ответ:
Пошаговое объяснение:
а) A(5;3), C(-4;15)
AC; y=kx+b;
3=5k+b;
15=-4k+b; 15-3=-4k-5k; 9k=-12; k=-12/9; k=-4/3=-1 1/3
3=5*(-4/3)+b; b=3+20/3; b=29/3=9 2/3
AC: y=-4/3 x+29/3
б) B(-11;-9), C(-4;15)
BC: y=kx+b;
уравнение перпендикуляа к стороне BC
⊥BC: y=-1/k *x+b
сторона BC:
-9=-11k+b;
15=-4k+b; 15-(-9)=-4k-(-11k); 24=7k; k=24/7=3,43; k=3,43
-9=-11*3,43+b; b=-9+37,73=28,73; b=28,73
BC: y=3,43x+28,73;
перпендикуляр к BC, проходящий через т.А
⊥BC(A): y=-0,29 *x+b
⊥BC(A): 3=-0,29*5+b; b=3+1,45=4,45
⊥BC(A): y=-0,29x+4,45;
точка пересечения перпендикуляра со стороной BC (т.D):
BC ∩ ⊥BC(A):
y=3,43x+28,73
y=-0,29x+4,45;
3,43x+28,73=-0,29x+4,45;
3,43x+0,29x=4,45-28,73;
3,72x=-24,28;
x=-24,28/3,72=-6,5;
y=3.43*(-6,5)+28,73=6,34;
D(-6,5;6,34)
A(5;3)
длина высоты - это расстояние между т А и D:
l AD l=√(5-(-6,5))²+(3-6,34)²)=√(132,25+11,15)=11,97;
l AD l≅12.
в) ∠B-?
∠B = ∠ между l AB l и l BC l
AB: y=kx+b;
3=5k+b;
-9=-11k+b; -9-3=-11k-5k; -12=-16k; k=-12/-16=0,75;
3=5*0,75+b; b=3-3,75=-0,75;
AB: y=0,75x-0,75;
BC: y=3,43x+28,73;
∠B=arctg3,43-arctg0.75=1,28-0,64=0,64 рад