Алгебра, вопрос задал kudryashka39 , 6 лет назад

задана функция у = - х квадрат + 8 х + с определить значение с при котором наибольшее значение функции с равно 7

Ответы на вопрос

Ответил AoiKuro

Ответ:

$\boxed{c=-9}$

Объяснение:

Запишем функцию:
$y=-x^2+8x+c$

Данная функция представляет из себя параболу, с ветвями опущенными вниз

Это означает что наивысшая точка параболы (максимум функции) лежит в точке вершины параболы с координатами (x₀; y₀), то есть

$f(x)_{max}=y_o=f(x_0)$

Согласно формуле $x_0=-\frac{b}{2a}$ , а $y_o=f(x_o)=f(\frac{-b}{2a} )$

Наше уравнение квадратное, в квадратном уравнение коэффициент при "x²" считают "a", при "x" - "b", а оставшееся - свободный член c

В нашем случае:
$a=-1\\b=8\\c=c$

Найдем x₀ нашей функции:

$x_0=-\frac{b}{2a}=\frac{-8}{-2} =4\\x_0=4$

Найдем y₀ функции:
$y_o=f(x_o)=f(\frac{-b}{2a} )=f(4)\\y_0=-16+32+c$

В нашем случае максимальное значение функции равно 7, подставим вместо y₀ семь, и решим уравнение

$y_0=-16+32+c\\7=-16+32+c\\c=-9$

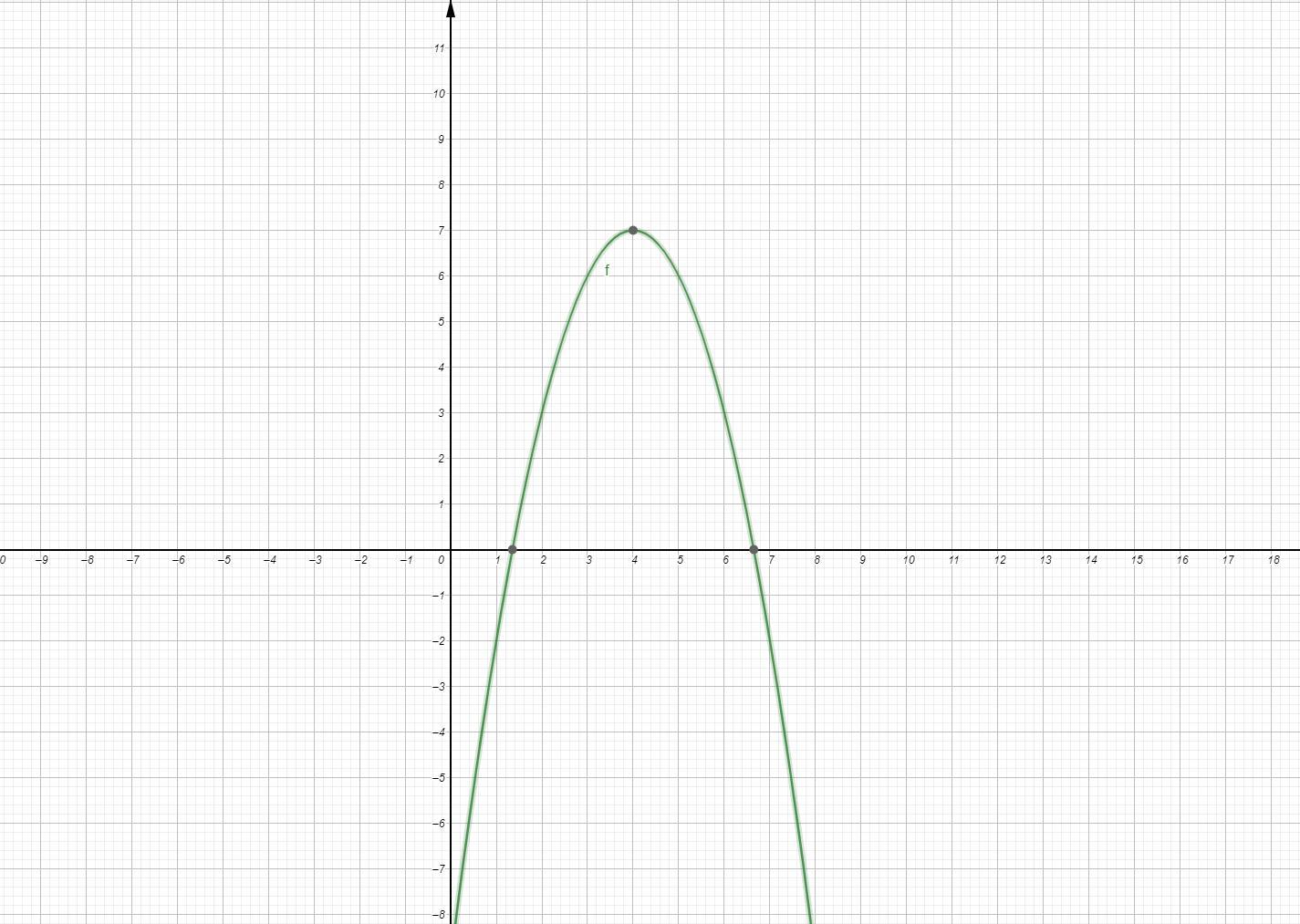
Состоит в построении графика и проверке вершины параболы

$f(x)=-x^2+8x-9$

Смотрите рисунок

Приложения:

Новые вопросы

Английский язык, 1 год назад

Русский язык, 1 год назад

Физика, 6 лет назад

Русский язык, 6 лет назад

Математика, 8 лет назад

Химия, 8 лет назад