ЗАДАЧА НА ЛОГИКУ 20 БАЛЛОВ
В апреле некоторого года три воскресенья пришлись на нечётные числа. Какой день недели был 20-го апреля? (Ответ Обосновать)
Ответы на вопрос
Ответ:
пятница
Объяснение:
Дни недели повторяются через 7 дней. Значит, если на этой неделе воскресенье было нечетное число, на следующей оно будет четное. В месяце должно быть пять воскресений, чтобы три из них могли совпасть с нечетными числами. Всего в апреле 30 дней, значит последним воскресеньем апреля с нечетным днем может быть только 29-е апреля (так как 30-е - четное число). Таким образом, если в апреле месяце последнее воскресенье - 29-е - нечетное, то нечетными будут 15-е и 1-е. Еще воскресенья в апреле будут 8-е и 22-е.
Значит, 20-е число в апреле месяце будет пятница.
Вот как например на файле в приложении.
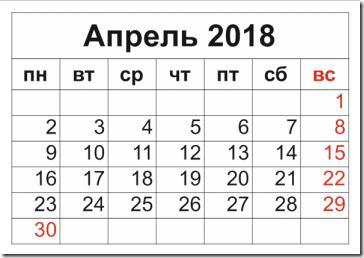
Ответ:
20 апреля будет пятница
Объяснение:
Каждое второе воскресенье будет чёстным, а всего может быть пять воскресения. Из них на не чётное должны попасть 3 значит подходит только если первое воскресенье попадёт на 1 число. Тогда 20 это пятница