Математика, вопрос задал lsokolovsckaya21 , 2 года назад

Задача 5.Срочно пожалуйста!!
Зоя заявила,что у неё в кармане вот столько грецких орехов:
пример
и она отдаст их тому,кто первым правильно назовёт их количество одним словом
Сколько у нее орехов?

Приложения:

serd2011: Какая из этих задач пятая?

lsokolovsckaya21: Первая,только если можно с объяснениями

serd2011: Там начало предложения обрезано. Либо замените картинку, либо допишите в вопрос само задание.

Ответы на вопрос

Ответил Аноним

Решение на фото/////

Приложения:

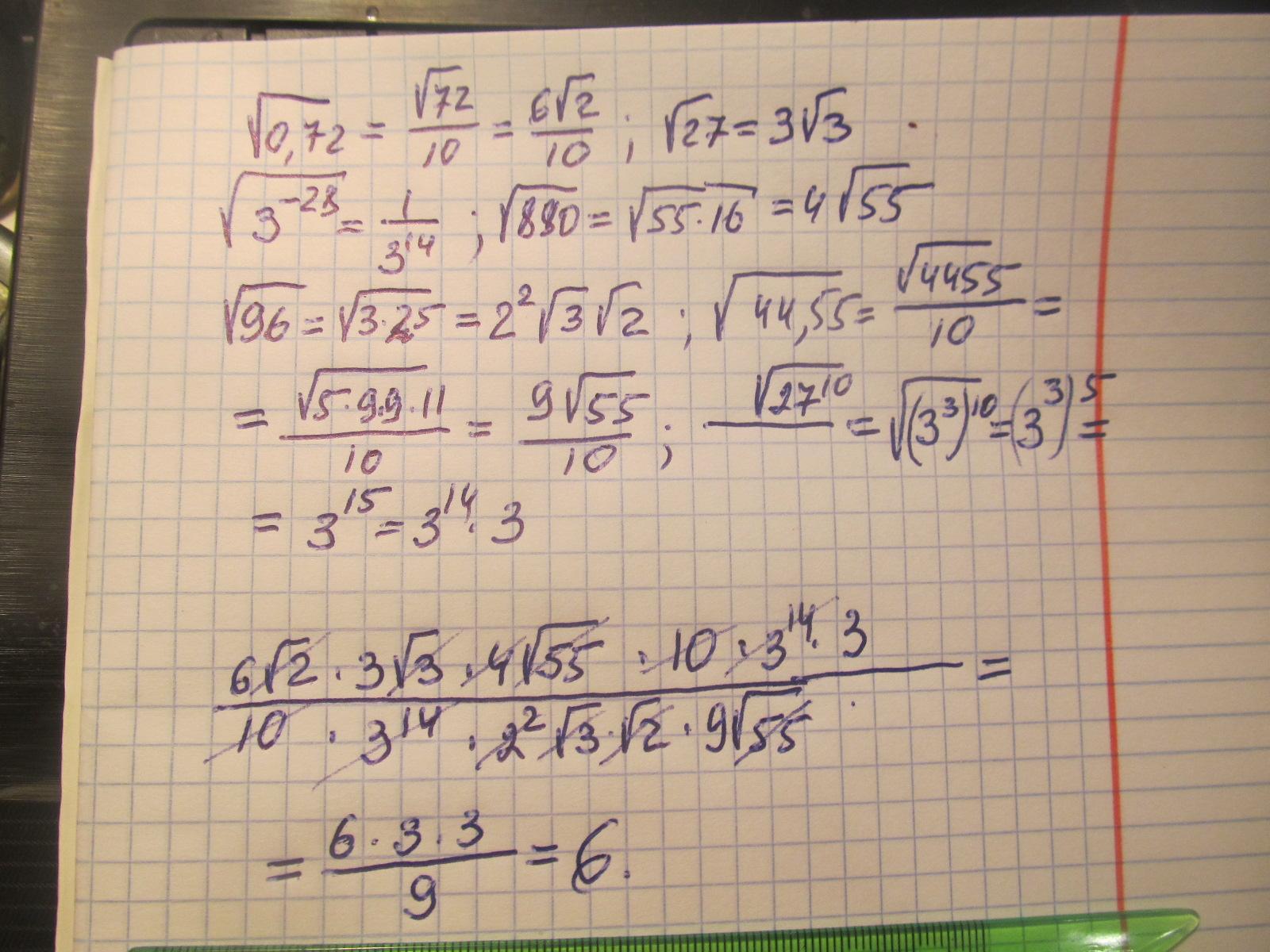
lsokolovsckaya21: Спасибо вам большое,а второе задание сможете решить?

lsokolovsckaya21: хорошо,спасибо большое)

lsokolovsckaya21: Ты проснулась?)

lsokolovsckaya21: совсем никак

Ответил serd2011

Ответ:

Пошаговое объяснение:

Чтобы ответить на вопрос нужно вычислить значение выражения

$\frac{\sqrt{0.72}*\sqrt{27}*\sqrt{3^{-28}}*\sqrt{880} }{\sqrt{96}*\sqrt{44.55}*\sqrt{27^{-10}}$

Выносим $3^{-28}$ и $27^{-10}$ из под корня

$\frac{\sqrt{0.72}*\sqrt{27}*\sqrt{3^{(-14)*2}}*\sqrt{880} }{\sqrt{96}*\sqrt{44.55}*\sqrt{27^{(-5)*2}} } = \frac{\sqrt{0.72}*\sqrt{27}*3^{(-14)}*\sqrt{880} }{\sqrt{96}*\sqrt{44.55}*27^{(-5)}$

Заменяем 27 на $3^3$

$\frac{\sqrt{0.72}*\sqrt{27}*3^{(-14)}*\sqrt{880} }{\sqrt{96}*\sqrt{44.55}*(3^3)^{(-5)} } = \frac{\sqrt{0.72}*\sqrt{27}*3^{(-14)}*\sqrt{880} }{\sqrt{96}*\sqrt{44.55}*3^{(-15)}$

$\frac{\sqrt{0.72}*\sqrt{27}*3^{(-14-(-15))}*\sqrt{880} }{\sqrt{96}*\sqrt{44.55} } = \frac{\sqrt{0.72}*\sqrt{27}*3^1*\sqrt{880} }{\sqrt{96}*\sqrt{44.55}$